Menu
> > >

川崎医科大学物理2012年第2問

次の問いに対して、最も適切なものを選択肢の中から一つ選びなさい。
  • I.時刻$t=0$に原点$\text{O}$を出発し、$x$軸上を正の方向に進む物体の運動を考える。物体が動き始めてからの時間$t$と、物体の加速度$a$との関係が図1のようになっているとき、物体の速度$v$を表すグラフの形は$\fbox{ア}$のようになる。ただし、縦軸の目盛りは省略してある。$v$は、$1\lt{t}\lt2$のとき$\fbox{イ}$、$2\lt{t}\lt3$のとき$\fbox{ウ}$、$8\lt{t}\lt9$のとき$\fbox{エ}$となる。また、物体の位置$x$は、$1\lt{t}\lt2$のとき$\fbox{オ}$、$2\lt{t}\lt3$のとき$\fbox{カ}$、$8\lt{t}\lt9$のとき$\fbox{キ}$と表せる。
    kawasakiika-2012-physics-2-1
    $\fbox{ア}$の選択肢
    kawasakiika-2012-physics-2-2
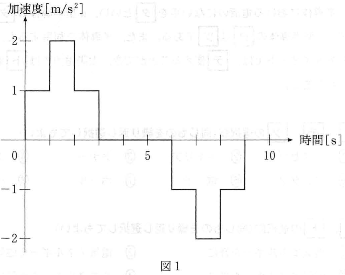
    $\fbox{イ}、\fbox{ウ}、\fbox{エ}$の選択肢（同じものを繰り返し選択してもよい）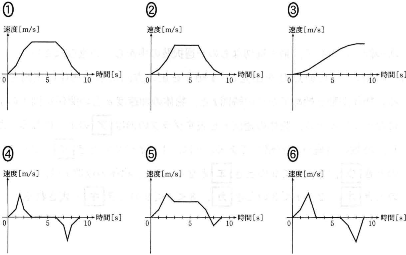
    • (1) $v=t$
    • (2) $v=t+1$
    • (3) $v=t-1$
    • (4) $v=2t+1$
    • (5) $v=2t-1$
    • (6) $v=t-9$
    • (7) $v=t+9$
    • (8) $v=-t+9$
    • (9) $v=-t-9$
    • (10) $v=2t-18$
    • (11) $v=-2t+18$
    • (12) $v=8$
    $\fbox{オ}、\fbox{カ}、\fbox{キ}$の選択肢（同じものを繰り返し選択してもよい）
    • (1) $x=\dfrac{1}{2}t^2$
    • (2) $x=t^2+1$
    • (3) $x=t^2-t+\dfrac{1}{2}$
    • (4) $x=\dfrac{1}{2}t^2+t-\dfrac{3}{2}$
    • (5) $x=-\dfrac{1}{2}t^2+9t-\dfrac{33}{2}$
    • (6) $x=t^2+t-\dfrac{1}{2}$
    • (7) $x=t^2+2t+1$
    • (8) $x=-t^2+t-\dfrac{1}{2}$
    • (9) $x=2t^2+18t-33$
    • (10) $x=2t^2+9t+17$
    • (11) $x=-\dfrac{1}{2}t^2+18t-\dfrac{17}{2}$
    • (12) $x=\dfrac{1}{2}t^2-9t+18$
  • II.雨の中、平らな地面に底面の面積が$S[\text{cm}^2]$の直方体容器を設置し、容器にたまった水の量を測定する。ただし、測定地の周辺で、雨は場所に依らず一様に降るものとし、水の密度を$1[\text{g}/\text{cm}^3]$とする。$1[\text{m}^2]$あたり1[L]（リットル）の雨が降るとき、容器にたまる水の深さ$d$は$\fbox{ク}[\text{mm}]$となる。また、$d=50[\text{mm}]$のとき、容器にたまった水の体積は、$\fbox{ケ}[\text{cm}^3]$で、$1[\text{m}^2]$あたりに降った雨の質量は、$\fbox{コ}[\text{kg}]$である。
    この容器にたまる水の深さを1時間毎に測定し、10時間の間の雨量の変化を調べたところ、図2に示すように、ある日には観測Aのような結果が得られ、別の日には観測Bのような結果が得られた。それぞれの日に降った雨の様子をグラフから読み取ると、観測開始後1時間の比較的短期的な平均雨量は、観測Aが$\fbox{サ}[\text{L}/(\text{m}^2\text{h})]$、観測Bが$\fbox{シ}[\text{L}/(\text{m}^2\text{h})]$であるが、全観測期間中の平均雨量は、観測Aが$\fbox{ス}[\text{L}/(\text{m}^2\text{h})]$、観測Bが$\fbox{セ}[\text{L}/(\text{m}^2\text{h})]$となる。
    kawasakiika-2012-physics-2-3
    $\fbox{ク}$の選択肢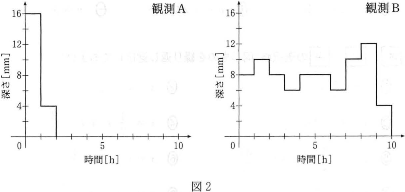
    • (1) $\dfrac{0.1}{S}$
    • (2) $0.1$
    • (3) $0.1S$
    • (4) $\dfrac{1}{S}$
    • (5) $1$
    • (6) $S$
    • (7) $\dfrac{10}{S}$
    • (8) $10$
    • (9) $10S$
    • (10) $\dfrac{100}{S}$
    • (11) $100$
    • (12) $100S$
    $\fbox{ケ}$の選択肢
    • (1) $\dfrac{0.5}{S}$
    • (2) $0.5$
    • (3) $0.5S$
    • (4) $\dfrac{5}{S}$
    • (5) $5$
    • (6) $5S$
    • (7) $\dfrac{50}{S}$
    • (8) $50$
    • (9) $50S$
    • (10) $\dfrac{500}{S}$
    • (11) $500$
    • (12) $500S$
    $\fbox{コ}$の選択肢
    • (1) $\dfrac{50}{S}$
    • (2) $50$
    • (3) $50S$
    • (4) $\dfrac{500}{S}$
    • (5) $500$
    • (6) $500S$
    • (7) $\dfrac{5000}{S}$
    • (8) $5000$
    • (9) $5000S$
    • (10) $\dfrac{50000}{S}$
    • (11) $50000$
    • (12) $50000S$
    $\fbox{サ}、\fbox{シ}、\fbox{ス}、\fbox{セ}$の選択肢(同じものを繰り返し選択してもよい)
    • (1) 0.8
    • (2) 1.6
    • (3) 3.2
    • (4) 2
    • (5) 4
    • (6) 8
    • (7) 10
    • (8) 16
    • (9) 32
    • (10) 80
    • (11) 100
    • (12) 160
  • III.図3のように、直列につながれた容量が$C_1, C_2, \cdots C_n$の$\text{n}$個のコンデンサーと電圧$V$の電池が接続されている。各コンデンサーに蓄えられる電荷を$Q_1, Q_2, \cdots, Q_n$、コンデンサーの極板間電圧を$V_1, V_2, \cdots V_n$とする。電池の電圧と各コンデンサーの極板間電圧との関係は$\fbox{ソ}$、各コンデンサーに蓄えられる電荷は$\fbox{タ}$とあらわされる。$\fbox{ソ}$と$\fbox{タ}$の関係から、$\fbox{チ}$が導き出される。
    一方、回路全体に蓄えられる電荷を$Q$とすると、各コンデンサーに蓄えられる電荷との関係は、$\fbox{ツ}$となる。よって、$\fbox{チ}$は$\fbox{テ}$と書き直すことができる。
    直列接続されたコンデンサーの合成容量を$C$とおくと、電圧$V$は$\fbox{ト}$となるので、$\fbox{テ}$と$\fbox{ト}$を比較することにより、合成容量$C$は$\fbox{ナ}$となる。 $\fbox{ソ}$の選択肢
    • (1) $V=V_1=V_2=\cdots=V_n$
    • (2) $V=V_1+V_2+\cdots+V_n$
    • (3) $\dfrac{1}{V}=\dfrac{1}{V_1}+\dfrac{1}{V_2}+\cdots+\dfrac{1}{V_n}$
    • (4) $\dfrac{1}{V}=V_1+V_2+\cdots+V_n$
    • (5) $V=\dfrac{1}{V_1}+\dfrac{1}{V_2}+\cdots+\dfrac{1}{V_n}$
    $\fbox{タ}$の選択肢
    • (1) $Q_1=C_1, Q_2=C_2, \cdots, Q_n=C_n$
    • (2) $Q_1=C_1V_1, Q_2=C_2V_2, \cdots, Q_n=C_nV_n$
    • (3) $Q_1=\dfrac{C_1}{V_1}, Q_2=\dfrac{C_2}{V_2}, \cdots, Q_n=\dfrac{C_n}{V_n}$
    • (4) $Q_1=\dfrac{V_1}{C_1}, Q_2=\dfrac{V_2}{C_2}, \cdots, Q_n=\dfrac{V_n}{C_n}$
    $\fbox{チ}$の選択肢
    • (1) $V=\dfrac{Q_1}{C_1}=\dfrac{Q_2}{C_2}=\cdots=\dfrac{Q_n}{C_n}$
    • (2) $V=\dfrac{Q_1}{C_1}+\dfrac{Q_2}{C_2}+\cdots+\dfrac{Q_n}{C_n}$
    • (3) $V=\dfrac{C_1}{Q_1}=\dfrac{C_2}{Q_2}=\cdots=\dfrac{C_n}{Q_n}$
    • (4) $V=\dfrac{C_1}{Q_1}+\dfrac{C_2}{Q_2}+\cdots+\dfrac{C_n}{Q_n}$
    • (5) $V=C_1Q_1+ C_2Q_2+ \cdots +C_nQ_n$
    $\fbox{ツ}$の選択肢
    • (1) $Q=Q_1=Q_2=\cdots=Q_n$
    • (2) $Q=Q_1+Q_2+\cdots+Q_n$
    • (3) $\dfrac{1}{Q}=\dfrac{1}{Q_1}+\dfrac{1}{Q_2}+\cdots+\dfrac{1}{Q_n}$
    • (4) $\dfrac{1}{Q}=Q_1+Q_2+\cdots+Q_n$
    • (5) $Q=\dfrac{1}{Q_1}+\dfrac{1}{Q_2}+\cdots+\dfrac{1}{Q_n}$
    $\fbox{テ}$の選択肢
    • (1) $V=\dfrac{Q}{C_1}=\dfrac{Q}{C_2}=\cdots=\dfrac{Q}{C_n}$
    • (2) $V=Q(\dfrac{1}{C_1}+\dfrac{1}{C_2}+\cdots+\dfrac{1}{C_n}) $
    • (3) $V=\dfrac{C_1}{Q}=\dfrac{C_2}{Q}=\cdots=\dfrac{C_n}{Q}$
    • (4) $V=\dfrac{1}{Q}(C_1+C_2+\cdots+C_n) $
    • (5) $V=Q(C_1+ C_2+ \cdots +C_n) $a
    $\fbox{ト}$の選択肢
    • (1) $V=\dfrac{Q}{C}$
    • (2) $V=\dfrac{C}{Q}$
    • (3) $V=CQ$
    $\fbox{ナ}$の選択肢
    • (1) $C=C_1=C_2=\cdots=C_n$
    • (2) $C=C_1+C_2+\cdots+C_n$
    • (3) $\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\cdots+\dfrac{1}{C_n}$
    • (4) $\dfrac{1}{C}=C_1+C_2+\cdots+C_n$
    • (5) $C=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\cdots+\dfrac{1}{C_n}$