慶應義塾大学物理2012年第3問
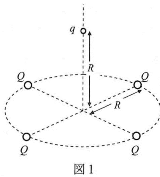
- 問1 図1に示すように、半径$R$の円の直交する直径の両端に点電荷$Q$を固定した。質量$m$の点電荷$q$を無限遠からゆっくり運び、円の中心から垂直距離$R$の位置に固定した。重力は無視でき、静電気のクーロンの法則の定数を$k_0$として、以下の問に答えよ。電荷$Q$、$q$は同符号とする。
- (1) 点電荷$q$を運ぶのに要した外力の仕事はいくらか。
- (2) 点電荷$q$の固定をはずした直後の点電荷$q$の加速度の大きさはいくらか。
- (3) 十分に時間が経ち一定になった点電荷$q$の速さはいくらか。
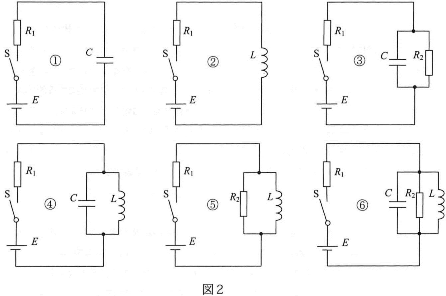
- 問2 図2に示すように、電圧$E$の電池、スイッチ$\text{S}$、抵抗値$R_1$、$R_2$の抵抗、電気容量$C$のコンデンサー、自己インダクタンス$L$のコイルを使い回路を作った。以下の1~3に答えよ。
- (1) 図の丸1~丸3について、$\text{S}$を閉じた直後に抵抗$R_1$を流れる電流はいくらか。ただし、$\text{S}$を閉じる直前のコンデンサーの電荷量は0である。
- (2) 図の丸1~丸3について、$\text{S}$を閉じて十分に時間が経ったとき、抵抗$R_1$を流れる電流は一定になった。その値を求めよ。
- (3) 図の丸3~丸6について、電池を交流電源に置き換えて$\text{S}$を閉じたところ、ある周波数のときにひとつの回路で抵抗$R_1$を流れる電流の振幅が0になった。どの回路かを答えよ。
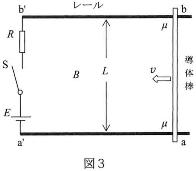
- 問3 図3に示すように、磁束密度$B$の一様な磁場中で、水平面内に置いた間隔$L$の2本の平行な金属レールの上に質量$M$の導体棒abをのせ、スイッチ$\text{S}$、抵抗$R$の抵抗、電圧$E$の電池を接続し回路を作った。レールおよび導体棒の抵抗はゼロであり、導体棒はレールに対して垂直な向きを保ったまま動く。重力加速度を$g$として以下の問に答えよ。
- (1) $\text{S}$を閉じたとき、導体棒にはレールに平行でaからa'の向きの力が働き動き出した。このときの磁束密度$B$の磁場の向きを以下の選択肢から選んで答えよ。
- (ア)鉛直下向き
- (イ )鉛直上向き
- (ウ)導体棒に平行でaからbの向き
- (エ)導体棒に平行でbからaの向き
- (オ)レールに平行でaからa'の向き
- (カ)レールに平行でa'からaの向き
- (2) $\text{S}$を閉じてしばらくすると、導体棒の速さ$v$は一定になった。このとき抵抗$R$を流れる電流$I$と導体棒の速さ$v$を求めよ。ただし、$\mu$、$M$、$g$、$R$、$B$、$L$、$E$のみを用いた式で答えよ。
- (3) 2の状態で電池が供給する電力を$P$、抵抗$R$で単位時間に発生するジュール熱を$Q_R$レールと導体棒の間で単位時間に発生する摩擦熱を$Q_\mu$とする。$P$、$Q_R$、$Q_\mu$のそれぞれを$\mu$、$M$、$g$、$R$、$B$、$L$、$E$を用いた式で表し、エネルギー保存の法則が成立することを説明せよ。
- (1) $\text{S}$を閉じたとき、導体棒にはレールに平行でaからa'の向きの力が働き動き出した。このときの磁束密度$B$の磁場の向きを以下の選択肢から選んで答えよ。