図1のように質量$m$と電荷$q$を持つ小球$\text{M}$を、長さが$l$で質量の無視できる細い棒の一端に取り付け、棒の他端を$\text{O}$とする。棒は固定された点$\text{O}$を中心に紙面内でなめらかに回転できる。鉛直線から棒へ反時計まわりにはかった角を$\theta$、重力加速度の大きさを$g$として、以下の問いに答えよ。

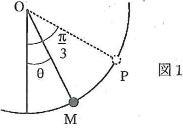
• (1) 水平方向右向きの電場を徐々に加えて電場の大きさが$E$となった時、$\theta=\dfrac{\pi}{3}$で小球$\text{M}$は静止した。この時の小球の位置を$\text{P}$とする。$E$および棒の張力$T$を$m$、$g$、$q$を用いて表せ。
以下では、(1)で加えた電場の大きさ$E$を保ったまま小球$\text{M}$の運動を考える。
• (2) 小球$\text{M}$を$\theta=\pi$まで持ち上げた後、静かにはなした。角$\theta$における重力による位置エネルギー$U_G$電場による位置エネルギー$U_E$を$m$、$g$、$l$、$\theta$で表せ。位置エネルギーの基準点は最下端の点($\theta=0$)とする。
• (3) 角$\theta$における小球$\text{M}$の速さ$v$を求めよ。
• (4) 小球$\text{M}$が動き始めてから最初に$v=0$となる時の$\theta$を、符号を含めて与えよ。必要であれば、下記の公式を使用せよ。 \[A\sin\theta+B\cos\theta=\sqrt{A^2+B^2}\sin(\theta+\alpha)\] ただし、$\alpha$は$\tan\alpha=\dfrac{B}{A}$を満たす角である。
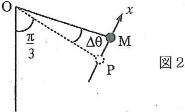
• (5) 図2のように点$\text{P}$を通り紙面内で$\text{OP}$に垂直な直線を$x$軸、点$\text{P}$を原点とする。$\theta$を$\dfrac{\pi}{3}$から微小変化させた後、静かにはなすと小球$\text{M}$は振動した。$\theta=\dfrac{\pi}{3}+\Delta\theta$の時、小球$\text{M}$に作用する、$x$軸方向の復元力の大きさを小球の座標値$x$で表し、振動の角振動数$\omega$を求めよ。必要であれば$\Delta\theta$が小さい時$\sin\Delta\theta\fallingdotseq\tan\Delta\theta\fallingdotseq\Delta\theta$、および$\cos\Delta\theta\fallingdotseq 1$の近似式が成立するとせよ。