図1のように$x-y$平面上で、$x$軸正方向へ進行する平面波$\text{A}$と負方向へ進行する平面波$\text{B}$を考える。波$\text{A}$と波$\text{B}$はともに波長$\lambda$、周期$T$、振幅$a$である。$x$軸上で$\text{OP}=\text{OQ}=L$となる点$\text{P}$と点$\text{Q}$において、波$\text{A}$と波$\text{B}$の振動は同じ(同位相)になっているとして、以下の問いに答えよ。

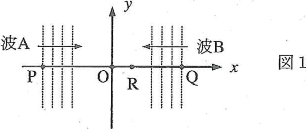
• (1) 原点$\text{O}$において、波$\text{A}$と波$\text{B}$は強め合うか、弱め合うか、そのいずれでもないかを答えよ。
• (2) 点$\text{R}(x,~0)$を通り$y$軸に平行な直線上において、波$\text{A}$と波$\text{B}$が強め合った。$\text{PR}$と$\text{QR}$の距離の差と波長$\lambda$の関係を、$x$と整数$m=0,1,2,3,\cdots$を用いて表せ。同様に弱め合う場合についても表せ。
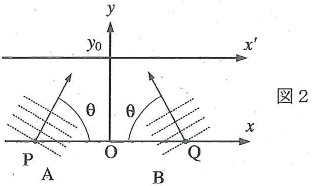
• (3) 図2に示すように波$\text{A}$が$x$軸正方向と角$\theta$の方向に進行している。(ここでは図にある波$\text{B}$をまだ考えない。)$y=y_0$において$y$軸と交わり$x$軸に平行な$x’$軸を取る。波$\text{A}$による変位は$x’$軸上を正方向に進行する。$x’$軸上を進行する波の波長$\lambda_x$、周期$T_x$、速さ$v_x$、振幅$a_x$を与えよ。
• (4) 波$\text{A}$による変位は$y$軸上を正方向に進行する。$y$軸上を進行する波の波長$\lambda_y$と速さ$v_y$を与えよ。
• (5) 波$\text{B}$を$x$軸負方向と角$\theta$の方向に進行させる。$x$軸上で$\text{OP}=\text{OQ}$となる点$\text{P}$と点$\text{Q}$において、波$\text{A}$と波$\text{B}$の振動は同じ(同位相)になっている。波$\text{B}$による変位は$x’$軸上を負方向に進行する。この波と(3)の$x’$軸上を正方向に進行する波が干渉して強め合うのはどこか。その$x$座標を波長$\lambda$、角$\theta$、整数$m=0,1,2,3,\cdots$を用いて表せ。
• (6) 下記の文が正しければ$\circ$を、誤っていれば$\times$を解答欄に記入せよ。
  • (a) $x=\pm\dfrac{1}{2}m\lambda_x$を通り$y$軸に平行な直線上では振幅$2a$、波長$\lambda_y$、速さ$v_y$の波が$y$軸正方向に進行する。
  • (b) $x=\pm\dfrac{1}{2}\left(m+\dfrac{1}{2}\right)\lambda_x$を通り$y$軸に平行な直線上では振幅$2a$、波長$\lambda_y$の定常波が発生する。
  • (c) $x$軸に平行な直線上では波長$\lambda_x$、周期$T_x$の波が進行する。