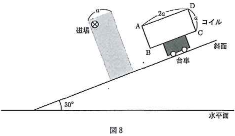
図8のように、水平面となす角度30$^\circ$のなめらかな斜面があり、斜面上には斜面に沿って長さ、$a$[m]にわたり、紙面の表から裏向きに、磁束密度の大きさ$B$[T]の一様な磁場が加わった領域がある。この斜面上に、縦$a$[m]、横$2a$[m]の長方形で全体の抵抗値が$R$[$\Omega$]の軽いコイル$\text{ABCD}$のついた質量$m$[kg]の台車を置いたところ、台車は斜面上をすべり降り、コイルの辺$\text{AB}$が磁場の中にある間は一定の速さで運動した。その後、コイルは磁場を通過した。ただし、重力加速度の大きさを$g$[m/s²]とし、すべての運動はコイルの面を含む鉛直面内で起こるものとする。また、コイルは台車に対して絶縁されており、台車は磁場に影響を与えないものとする。

• 問1 磁場に侵入したときのコイルの速さを$v_0$[m/s]とする。コイルの辺$\text{AB}$が磁場に進入した直後にコイルを流れる電流は$\fbox{23}$の向きで、その大きさ$v_0$を含む式で表すと$\fbox{24}$[A]である。また、コイルが磁場から受ける力の大きさを$v_0$を含む式で表すと$\fbox{25}$[N]である。
  $\fbox{23}$の解答群
  • (1) $\fbox{A}$→$\fbox{B}$→$\fbox{C}$→$\fbox{D}$→$\fbox{A}$
  • (2) $\fbox{A}$→$\fbox{D}$→$\fbox{C}$→$\fbox{B}$→$\fbox{A}$
  $\fbox{24}$と$\fbox{25}$の解答群
  • (1) $\dfrac{aBv_0}{R}$
  • (2) $\dfrac{2aBv_0}{R}$
  • (3) $\dfrac{a^2Bv_0}{R}$
  • (4) $\dfrac{4a^2Bv_0}{R}$
  • (5) $\dfrac{aB^2v_0}{R}$
  • (6) $\dfrac{2aB^2v_0}{R}$
  • (7) $\dfrac{aB{v_0}^2}{R}$
  • (8) $\dfrac{2aB{v_0}^2}{R}$
  • (9) $\dfrac{a^2B^2v_0}{R}$
  • (10) $\dfrac{4a^2B^2v_0}{R}$
  • (11) $\dfrac{a^2B^2{v_0}^2}{R}$
  • (12) $\dfrac{4a^2B^2{v_0}^2}{R}$
• 問2 コイルの辺$\text{AB}$が磁場中にあるときの台車の速さは$\fbox{26}$[m/s]であり、このときコイルで消費される電力は$\fbox{27}$[W]である。
  $\fbox{26}$の解答群
  • (1) $\dfrac{mgR}{2aB}$
  • (2) $\dfrac{mgR}{2a^2B^2}$
  • (3) $\dfrac{mgaB}{2R}$
  • (4) $\dfrac{mga^2B^2}{2R}$
  • (5) $\dfrac{mgR}{aB}$
  • (6) $\dfrac{mgR}{a^2B^2}$
  • (7) $\dfrac{mgaB}{R}$
  • (8) $\dfrac{mga^2B^2}{R}$
  • (9) $\dfrac{\sqrt{3}mgR}{2aB}$
  • (10) $\dfrac{\sqrt{3}mgR}{a^2B^2}$
  • (11) $\dfrac{\sqrt{3}mgaB}{2R}$
  • (12) $\dfrac{\sqrt{3}mgaB}{2R}$
  $\fbox{27}$の解答群
  • (1) $\dfrac{R}{4}\left(\dfrac{mg}{aB}\right)^2$
  • (2) $\dfrac{R}{4}\left(\dfrac{mg}{a^2B^2}\right)^2$
  • (3) $\dfrac{1}{4R}\left(\dfrac{mg}{aB}\right)^2$
  • (4) $\dfrac{1}{4R}\left(\dfrac{mg}{a^2B^2}\right)^2$
  • (5) $R\left(\dfrac{mg}{aB}\right)^2$
  • (6) $R\left(\dfrac{mg}{a^2B^2}\right)^2$
  • (7) $\dfrac{1}{R}\left(\dfrac{mg}{aB}\right)^2$
  • (8) $\dfrac{1}{R}\left(\dfrac{mg}{a^2B^2}\right)^2$
  • (9) $\dfrac{3R}{4}\left(\dfrac{mg}{aB}\right)^2$
  • (10) $\dfrac{3R}{4}\left(\dfrac{mg}{a^2B^2}\right)^2$
  • (11) $\dfrac{4R}{3}\left(\dfrac{mg}{aB}\right)^2$
  • (12) $\dfrac{4R}{3}\left(\dfrac{mg}{a^2B^2}\right)^2$
• 問3 コイルの辺$\text{AB}$が磁場に入ってから磁場から出るまでにコイルで発生したジュール熟は$\fbox{28}$[J]である。
  解答群
  • (1) $\dfrac{mg}{2}$
  • (2) $mg$
  • (3) $\dfrac{mga}{2}$
  • (4) $mga$
  • (5) $\dfrac{mgB}{2}$
  • (6) $mgB$
  • (7) $\dfrac{mgaB}{2}$
  • (8) $mgaB$
  • (9) $\dfrac{mgB}{2R}$
  • (10) $\dfrac{mgB}{R}$
  • (11) $\dfrac{mgaB}{2R}$
  • (12) $\dfrac{mgaB}{R}$
  • (13) $\dfrac{aB}{mgR}$
  • (14) $\dfrac{aB}{2mgR}$
  • (15) $\dfrac{a^2B^2}{mgR}$
  • (16) $\dfrac{a^2B^2}{2mgR}$
• 問4 コイルの辺$\text{CD}$が磁場に入った直後にコイルが磁場から受ける力の大きさは$\fbox{29}$[N]である。
  解答群
  • (1) $\dfrac{1}{2}mg$
  • (2) $mg$
  • (3) $\dfrac{a^2B^2}{R}\sqrt{ag}$
  • (4) $\dfrac{a^2B^2}{R}\sqrt{2ag}$
  • (5) $\dfrac{2a^2B^2}{R}\sqrt{ag}$
  • (6) $\dfrac{1}{2}mg+\dfrac{a^2B^2}{R}\sqrt{ag}$
  • (7) $\dfrac{1}{2}mg+\dfrac{2a^2B^2}{R}\sqrt{ag}$
  • (8) $\dfrac{1}{2}mg+\dfrac{2a^2B^2}{R}\sqrt{ag}$
  • (9) $mg+\dfrac{a^2B^2}{R}\sqrt{ag}$
  • (10) $mg+\dfrac{a^2B^2}{R}\sqrt{2ag}$
  • (11) $mg+\dfrac{2a^2B^2}{R}\sqrt{ag}$
  • (12) $\sqrt{\left(\dfrac{mg}{2}\right)^2+ag\left(\dfrac{a^2B^2}{R}\right)^2}$
  • (13) $\sqrt{\left(\dfrac{mg}{2}\right)^2+2ag\left(\dfrac{a^2B^2}{R}\right)^2}$
  • (14) $\sqrt{\left(\dfrac{mg}{2}\right)^2+4ag\left(\dfrac{a^2B^2}{R}\right)^2}$
  • (15) $\sqrt{\left(mg\right)^2+ag\left(\dfrac{a^2B^2}{R}\right)^2}$
  • (16) $\sqrt{\left(mg\right)^2+2ag\left(\dfrac{a^2B^2}{R}\right)^2}$
  • (17) $\sqrt{\left(mg\right)^2+4ag\left(\dfrac{a^2B^2}{R}\right)^2}$
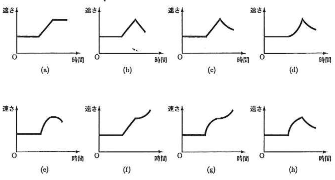
• 問5 コイルの辺$\text{AB}$が磁場に入ってから辺$\text{CD}$が磁場から出るまでの、台車の速さの変化のようすをもっともよく表しているグラフは$\fbox{30}$である。
  解答群