北里大学物理2012年第2問
次の問い(1~7)の空所に入る適語を解答群から選択せよ。$\big($解答番号$\fbox{22}$~$\fbox{29}\big)$
図5のように、矢印の向きに一定の加速度で加速している電車の天井に、ばね定数$k$ [N/m]の軽いばね$\text{A}$をつり下げ、下端に質量$m$[kg]の小さな皿$\text{B}$を取り付けた。さらに、$\text{B}$の上に質量$M$[kg]の小物体$\text{C}$を静かに載せたところ、鉛直から角度$\theta$ radだけ傾いて$\text{A}$、$\text{B}$、$\text{C}$は静止した。ただし、$\text{A}$、$\text{B}$、$\text{C}$の運動は電車内にいる人が観測するものとし、重力加速度の大きさを$g[\text{m}/\text{s}^2]$とする。
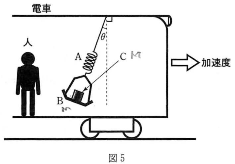

- 電車の加速度の大きさを電車の外の人が観測すると$\fbox{22}[\text{m}/\text{s}^2]$である。
解答群
- (1) $g\tan\theta$
- (2) $g(1+\tan\theta)$
- (3) $g(1-\tan\theta)$
- (4) $g\sqrt{1+\tan^2\theta}$
- (5) $g\sqrt{1-\tan^2\theta}$
- (6) $\dfrac{g}{\tan\theta}$
- (7) $\dfrac{g}{1+\tan\theta}$
- (8) $\dfrac{g}{1-\tan\theta}$
- (9) $\dfrac{g}{\sqrt{1+\tan^2\theta}}$
- (10) $\dfrac{g}{\sqrt{1-\tan^2\theta}}$
- $\text{A}$は自然な長さから$\fbox{23}$[m]だけのびている。
解答群
- (1) $\dfrac{Mg}{k}\cdot\tan\theta$
- (2) $\dfrac{Mg}{k}\cdot\sqrt{1+\tan^2\theta}$
- (3) $\dfrac{Mg}{k}\cdot\sqrt{1-\tan^2\theta}$
- (4) $\dfrac{mg}{k}\cdot\tan\theta$
- (5) $\dfrac{mg}{k}\cdot\sqrt{1+\tan^2\theta}$
- (6) $\dfrac{mg}{k}\cdot\sqrt{1-\tan^2\theta}$
- (7) $\dfrac{(M+m)g}{k}\cdot\tan\theta$
- (8) $\dfrac{(M+m)g}{k}\cdot\sqrt{1+\tan^2\theta}$
- (9) $\dfrac{(M+m)g}{k}\cdot\sqrt{1-\tan^2\theta}$
- つぎに、角度$\theta$を保ったまま$\text{A}$をさらに$\text{L}$[m]だけ引きのばして静かに放したところ、$\text{B}$と$\text{C}$は一体となって単振動を始めた。このときの単振動の周期は$\fbox{24}$[s]である。
解答群
- (1) $2\pi\sqrt{\dfrac{M}{k}}$
- (2) $2\pi\sqrt{\dfrac{m}{k}}$
- (3) $2\pi\sqrt{\dfrac{M+m}{k}}$
- (4) $2\pi\tan\theta\sqrt{\dfrac{M}{k}}$
- (5) $2\pi\tan\theta\sqrt{\dfrac{m}{k}}$
- (6) $2\pi\tan\theta\sqrt{\dfrac{M+m}{k}}$
- (7) $2\pi\sqrt{\dfrac{M(1+\tan^2\theta)}{k}}$
- (8) $2\pi\sqrt{\dfrac{m(1+\tan^2\theta)}{k}}$
- (9) $2\pi\sqrt{\dfrac{(M+m)(1+\tan^2\theta)}{k}}$
- (10) $2\pi\sqrt{\dfrac{M(1-\tan^2\theta)}{k}}$
- (11) $2\pi\sqrt{\dfrac{m(1-\tan^2\theta)}{k}}$
- (12) $2\pi\sqrt{\dfrac{(M+m)(1-\tan^2\theta)}{k}}$
- 3.の状態で、$\text{B}$の速さの最大値は$\fbox{25}$[m/s]である。
解答群
- (1) $L\sqrt{\dfrac{M}{k}}$
- (2) $L\sqrt{\dfrac{m}{k}}$
- (3) $L\sqrt{\dfrac{M+m}{k}}$
- (4) $L\sqrt{\dfrac{k}{M}}$
- (5) $L\sqrt{\dfrac{k}{m}}$
- (6) $L\sqrt{\dfrac{k}{M+m}}$
- (7) $g\sqrt{\dfrac{M(1+\tan^2\theta)}{k}}$
- (8) $g\sqrt{\dfrac{m(1+\tan^2\theta)}{k}}$
- (9) $g\sqrt{\dfrac{(M+m)(1+\tan^2\theta)}{k}}$
- (10) $g\sqrt{\dfrac{k(1+\tan^2\theta)}{M}}$
- (11) $g\sqrt{\dfrac{k(1+\tan^2\theta)}{m}}$
- (12) $g\sqrt{\dfrac{k(1+\tan^2\theta)}{M+m}}$
- 3.の状態で、$\text{A}$がもっとも縮んだとき、$\text{C}$に生じている加速度の大きさは$\fbox{26}[\text{m}/\text{s}^2]$である。
解答群
- (1) $\dfrac{M}{k}\cdot{L}$
- (2) $\dfrac{m}{k}\cdot{L}$
- (3) $\dfrac{M+m}{k}\cdot{L}$
- (4) $\dfrac{k}{M}\cdot{L}$
- (5) $\dfrac{k}{m}\cdot{L}$
- (6) $\dfrac{k}{M+m}\cdot{L}$
- (7) $g+\dfrac{M}{k}\cdot{L}$
- (8) $g+\dfrac{m}{k}\cdot{L}$
- (9) $g+\dfrac{M+m}{k}\cdot{L}$
- (10) $g+\dfrac{k}{M}\cdot{L}$
- (11) $g+\dfrac{k}{m}\cdot{L}$
- (12) $g+\dfrac{k}{M+m}\cdot{L}$
- 5.の状態で、$\text{C}$が$\text{B}$から受ける垂直抗力の大きさは$\fbox{27}$[N]であり、$\text{C}$と$\text{B}$が一体となって運動しているため、3.でのばした長さ$\text{L}$は$\fbox{28}$[m]以下でなければならない。
$\fbox{27}$の解答群
- (1) $\dfrac{M}{mk}\cdot{L}$
- (2) $\dfrac{m}{Mk}\cdot{L}$
- (3) $\dfrac{M+m}{Mk}\cdot{L}$
- (4) $\dfrac{M+m}{mk}\cdot{L}$
- (5) $\dfrac{mk}{M}\cdot{L}$
- (6) $\dfrac{Mk}{m}\cdot{L}$
- (7) $\dfrac{Mk}{M+m}\cdot{L}$
- (8) $\dfrac{mk}{M+m}\cdot{L}$
- (9) $Mg\sqrt{1+\tan^2\theta}-\dfrac{M}{mk}\cdot{L}$
- (10) $Mg\sqrt{1+\tan^2\theta}-\dfrac{m}{Mk}\cdot{L}$
- (11) $Mg\sqrt{1+\tan^2\theta}-\dfrac{M+m}{Mk}\cdot{L}$
- (12) $Mg\sqrt{1+\tan^2\theta}-\dfrac{M+m}{mk}\cdot{L}$
- (13) $Mg\sqrt{1+\tan^2\theta}-\dfrac{mk}{M}\cdot{L}$
- (14) $Mg\sqrt{1+\tan^2\theta}-\dfrac{Mk}{m}\cdot{L}$
- (15) $Mg\sqrt{1+\tan^2\theta}-\dfrac{Mk}{M+m}\cdot{L}$
- (16) $Mg\sqrt{1+\tan^2\theta}-\dfrac{mk}{M+m}\cdot{L}$
- (1) $\dfrac{M}{k}\cdot{g}\sqrt{1+\tan^2\theta}$
- (2) $\dfrac{m}{k}\cdot{g}\sqrt{1+\tan^2\theta}$
- (3) $\dfrac{M+m}{k}\cdot{g}\sqrt{1+\tan^2\theta}$
- (4) $\dfrac{k}{M}\cdot{g}\sqrt{1+\tan^2\theta}$
- (5) $\dfrac{k}{m}\cdot{g}\sqrt{1+\tan^2\theta}$
- (6) $\dfrac{k}{M+m}\cdot{g}\sqrt{1+\tan^2\theta}$
- (7) $\dfrac{2M}{k}\cdot{g}\sqrt{1+\tan^2\theta}$
- (8) $\dfrac{2m}{k}\cdot{g}\sqrt{1+\tan^2\theta}$
- (9) $\dfrac{2(M+m)}{k}\cdot{g}\sqrt{1+\tan^2\theta}$
- (10) $\dfrac{2k}{M}\cdot{g}\sqrt{1+\tan^2\theta}$
- (11) $\dfrac{2k}{m}\cdot{g}\sqrt{1+\tan^2\theta}$
- (12) $\dfrac{2k}{M+m}\cdot{g}\sqrt{1+\tan^2\theta}$
- 5.の状態で、$\text{C}$がもっている重力による位置エネルギーは$\fbox{29}[\text{J}]$である。ただし、位置エネルギーの基準は、$\text{B}$の速さが最大となったときの$\text{C}$の位置とする。
解答群
- (1) $MgL\sin\theta$
- (2) $mgL\sin\theta$
- (3) $(M+m)gL\sin\theta$
- (4) $MgL\cos\theta$
- (5) $mgL\cos\theta$
- (6) $(M+m)gL\cos\theta$
- (7) $MgL\tan\theta$
- (8) $mgL\tan\theta$
- (9) $(M+m)gL\tan\theta$
- (10) $MgL\sqrt{1+\tan^2\theta}$
- (11) $mgL\sqrt{1+\tan^2\theta}$
- (12) $(M+m)gL\sqrt{1+\tan^2\theta}$
- (13) $MgL\sqrt{1-\tan^2\theta}$
- (14) $mgL\sqrt{1-\tan^2\theta}$
- (15) $(M+m)gL\sqrt{1-\tan^2\theta}$