次の問い（1～7）の空所に入る適語を解答群から選択せよ。$\big($解答番号$\fbox{30}$～$\fbox{42}\big)$
図6のように、半径を自由に変えることのできる球形の断熱容器に、絶対温度$T$[K]で質量$m$[kg]の単原子分子からなる理想気体が$n$[mol]だけ入っている。ただし、図には、速さ$v$[m/s]の1つの気体分子$\text{A}$が容器の壁に入射角$\theta$ radで衝突してはね返っているようすを、分子の速度ベクトルと容器の中心をふくむ平面内で描いてある。はじめ、容器の半径は$r$ [m]に固定されており、すべての気体分子は壁と弾性衡突するものとし、気体分子どうしの衡突は考えないものとする。また、気体定数は$R[\text{J}/(\text{mol}\cdot\text{K})]$とする。

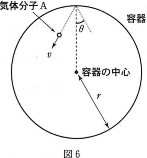
1. $\text{A}$の衝突前後での運動量変化の大きさは$\fbox{30}$[kg・m/s]である。
   $\fbox{30}$の解答群
   • (1) $\dfrac{1}{2}mv$
   • (2) $mv$
   • (3) $2mv$
   • (4) $\dfrac{1}{2}mv\cos\theta$
   • (5) $mv\cos\theta$
   • (6) $2mv\cos\theta$
   • (7) $\dfrac{1}{2}mv\sin\theta$
   • (8) $mv\sin\theta$
   • (9) $2mv\sin\theta$
   • (10) $\dfrac{1}{2}mv\tan\theta$
   • (11) $mv\tan\theta$
   • (12) $2mv\tan\theta$
2. $\text{A}$が時間$t$[s]の間に容器の壁と衝突する回数は$\fbox{31}\times{t}$回である。
   $\fbox{31}$の解答群
   • (1) $\dfrac{v}{2r}$
   • (2) $\dfrac{v}{r}$
   • (3) $\dfrac{2v}{r}$
   • (4) $\dfrac{v\cos\theta}{2r}$
   • (5) $\dfrac{v\cos\theta}{r}$
   • (6) $\dfrac{2v\cos\theta}{r}$
   • (7) $\dfrac{v}{2r\cos\theta}$
   • (8) $\dfrac{v}{r\cos\theta}$
   • (9) $\dfrac{2v}{r\cos\theta}$
   • (10) $\dfrac{v\sin\theta}{2r}$
   • (11) $\dfrac{v\sin\theta}{r}$
   • (12) $\dfrac{2v\sin\theta}{r}$
   • (13) $\dfrac{v}{2r\sin\theta}$
   • (14) $\dfrac{v}{r\sin\theta}$
   • (15) $\dfrac{2v}{r\sin\theta}$
3. $\text{A}$が時間$t$の間に壁に及ぼす力の大きさの平均は$\fbox{32}$[N]である。
   $\fbox{32}$の解答群
   • (1) $\dfrac{mv}{2r}$
   • (2) $\dfrac{mv}{r}$
   • (3) $\dfrac{2mv}{r}$
   • (4) $\dfrac{mv^2}{2r}$
   • (5) $\dfrac{mv^2}{r}$
   • (6) $\dfrac{2mv^2}{r}$
   • (7) $\dfrac{mv\tan\theta}{2r}$
   • (8) $\dfrac{mv\tan\theta}{r}$
   • (9) $\dfrac{2mv\tan\theta}{r}$
   • (10) $\dfrac{mv^2\tan\theta}{2r}$
   • (11) $\dfrac{mv^2\tan\theta}{r}$
   • (12) $\dfrac{2mv^2\tan\theta}{r}$
   • (13) $\dfrac{mv}{2r\tan\theta}$
   • (14) $\dfrac{mv}{r\tan\theta}$
   • (15) $\dfrac{2mv}{r\tan\theta}$
   • (16) $\dfrac{mv^2}{2r\tan\theta}$
   • (17) $\dfrac{mv^2}{r\tan\theta}$
   • (18) $\dfrac{2mv^2}{r\tan\theta}$
4. 容器内にある$n$[mol]の気体分子の個数を$N$とし、気体分子の速さの2乗を$N$個の気体分子で平均したものを$(v^2)[\text{m}^2/\text{s}^2]$とおく。このとき、気体の圧力を、容器の体積$V[\text{m}^3]$、$m$、$N$、$(v^2)$を用いて表すと、$\fbox{33}$[Pa]となる。
   $\fbox{33}$の解答群
   • (1) $\dfrac{NmV}{3(v^2)}$
   • (2) $\dfrac{NmV}{2(v^2)}$
   • (3) $\dfrac{2NmV}{3(v^2)}$
   • (4) $\dfrac{NmV}{(v^2)}$
   • (5) $\dfrac{3NmV}{2(v^2)}$
   • (6) $\dfrac{2NmV}{(v^2)}$
   • (7) $\dfrac{3NmV}{(v^2)}$
   • (8) $\dfrac{Nm(v^2)}{3V}$
   • (9) $\dfrac{Nm(v^2)}{2V}$
   • (10) $\dfrac{2Nm(v^2)}{3V}$
   • (11) $\dfrac{Nm(v^2)}{V}$
   • (12) $\dfrac{3Nm(v^2)}{2V}$
   • (13) $\dfrac{2Nm(v^2)}{V}$
   • (14) $\dfrac{3Nm(v^2)}{V}$
5. 気体分子全体がもっている運動エネルギーを$n$、$R$、$T$を用いて表すと$\fbox{34}[\text{J}]$となる。
   $\fbox{34}$の解答群
   • (1) $\dfrac{nR}{3T}$
   • (2) $\dfrac{nR}{2T}$
   • (3) $\dfrac{2nR}{3T}$
   • (4) $\dfrac{nR}{T}$
   • (5) $\dfrac{3nR}{2T}$
   • (6) $\dfrac{2nR}{T}$
   • (7) $\dfrac{3nR}{T}$
   • (8) $\dfrac{nRT}{3}$
   • (9) $\dfrac{nRT}{2}$
   • (10) $\dfrac{2nRT}{3}$
   • (11) $nRT$
   • (12) $\dfrac{3nRT}{2}$
   • (13) $2nRT$
   • (14) $3nRT$
6. 容器の半径を固定したまま、$Q[\text{J}]$の熱を外から気体に加える。このとき、気体分子が容器の壁に及ぼす圧力は$\fbox{35}\times\fbox{36}\times{Q}$[Pa]だけ変化し、温度は$\fbox{37}\times\fbox{38}\times{Q}$[K]だけ変化する。
   $\fbox{35}$と$\fbox{37}$の解答群
   • (1) $\dfrac{1}{4}$
   • (2) $\dfrac{1}{3}$
   • (3) $\dfrac{2}{5}$
   • (4) $\dfrac{1}{2}$
   • (5) $\dfrac{3}{5}$
   • (6) $\dfrac{2}{3}$
   • (7) $\dfrac{3}{4}$
   • (8) $1$
   • (9) $\dfrac{4}{3}$
   • (10) $\dfrac{3}{2}$
   • (11) $\dfrac{5}{3}$
   • (12) $2$
   • (13) $\dfrac{5}{2}$
   $\fbox{36}$と$\fbox{38}$の解答群
   • (1) $R$
   • (2) $n$
   • (3) $V$
   • (4) $\dfrac{1}{R}$
   • (5) $\dfrac{1}{n}$
   • (6) $\dfrac{1}{V}$
   • (7) $nR$
   • (8) $nV$
   • (9) $VR$
   • (10) $\dfrac{1}{nR}$
   • (11) $\dfrac{1}{nV}$
   • (12) $\dfrac{1}{VR}$
   • (13) $nRV$
   • (14) $\dfrac{1}{nRV}$
7. 6. で熱を加える前の状態にもどし、気体の圧力が容器の外の圧力とつり合うように、容器の半径が自由に変化できる状態にしたところ、容器の半径は$r$のままであった。さらに、気体に熱を加えたところ、温度が$\Delta{T}$[K]だけ変化した。このとき、気体がした仕事は$\fbox{39}\times\fbox{40}\times\Delta{T}[\text{J}]$であり、気体に加えた熱量は$\fbox{41}\times\fbox{42}\times\Delta{T}[\text{J}]$である。
   $\fbox{39}$と$\fbox{41}$の解答群
   • (1) $\dfrac{1}{4}$
   • (2) $\dfrac{1}{3}$
   • (3) $\dfrac{2}{5}$
   • (4) $\dfrac{1}{2}$
   • (5) $\dfrac{3}{5}$
   • (6) $\dfrac{2}{3}$
   • (7) $\dfrac{3}{4}$
   • (8) $1$
   • (9) $\dfrac{4}{3}$
   • (10) $\dfrac{3}{2}$
   • (11) $\dfrac{5}{3}$
   • (12) $2$
   • (13) $\dfrac{5}{2}$
   $\fbox{40}$と$\fbox{42}$の解答群
   • (1) $R$
   • (2) $n$
   • (3) $V$
   • (4) $\dfrac{1}{R}$
   • (5) $\dfrac{1}{n}$
   • (6) $\dfrac{1}{V}$
   • (7) $nR$
   • (8) $nV$
   • (9) $VR$
   • (10) $\dfrac{1}{nR}$
   • (11) $\dfrac{1}{nV}$
   • (12) $\dfrac{1}{VR}$
   • (13) $nRV$
   • (14) $\dfrac{1}{nRV}$