四角にあてはまる最も適当なものを対応する解答群の中から一つずつ選べ。
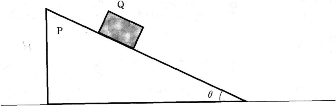
図のように、水平な床の上に質量$M$[kg]の三角柱$\text{P}$が静止している。傾き$\theta$の$\text{P}$の斜面上に質量$m$[kg]の物体$\text{Q}$をのせて静かに手を放すと、$\text{P}$は水平方向に、$\text{Q}$は斜面に沿って同時に動き出した。ただし、$M{\gt}m$とする、また、床と$\text{P}$の間、および$\text{P}$と$\text{Q}$の間に摩擦力ははたらかないとする。重力加速度の大きさを$g$[m/s²]とする。

• (a) 床に対する$\text{P}$の加速度の大きさを$A$[m/s²]、$\text{P}$から見た$\text{Q}$の加速度の大きさを$a$[m/s²]、$\text{Q}$にはたらく垂直抗力の大きさを$N$[N]とすると、$MA=\fbox{ア}$、$ma=\fbox{イ}$が成り立つ。また、$\text{P}$から見た$\text{Q}$にはたらく力の、斜面に垂直な成分について、$N=\fbox{ウ}$が成り立つ。
  以上の関係を用いると、$A=\fbox{エ}$、$a=\fbox{オ}$、$N=\fbox{カ}$と表される。
  • $\fbox{ア}$の解答群
    • (1) $Mg$
    • (2) $Mg+N\sin\theta$
    • (3) $Mg\sin\theta+N\cos\theta$
    • (4) $Mg\cos\theta+N$
    • (5) $N$
    • (6) $N\sin\theta$
    • (7) $N\cos\theta$
    • (8) $mg\cos\theta$
    • (9) $mg\cos\theta\sin\theta$
    • (0) $mg\cos\theta\sin\theta+N\sin\theta$
  • $\fbox{イ}$の解答群
    • (1) $mg\sin\theta$
    • (2) $mg\sin\theta+mA$
    • (3) $mg\sin\theta-mA$
    • (4) $mg\sin\theta+ma\sin\theta$
    • (5) $mg\sin\theta-mA\sin\theta$
    • (6) $mg\sin\theta+mA\cos\theta$
    • (7) $mg\sin\theta-mA\cos\theta$
    • (8) $mg\sin\theta+MA$
    • (9) $mg\sin\theta+MA\cos\theta$
    • (0) $mg\sin\theta-MA\sin\theta$
  • $\fbox{ウ}$の解答群
    • (1) $mg\sin\theta$
    • (2) $mg\cos\theta$
    • (3) $mg\sin\theta+mA$
    • (4) $mg\cos\theta+mA$
    • (5) $mg\sin\theta-mA$
    • (6) $mg\cos\theta-mA$
    • (7) $mg\sin\theta+mA\cos\theta$
    • (8) $mg\cos\theta+mA\sin\theta$
    • (9) $mg\sin\theta-mA\cos\theta$
    • (0) $mg\cos\theta-mA\sin\theta$
  • $\fbox{エ}$の解答群
    • (1) $g$
    • (2) $\dfrac{m}{M}g\cos\theta$
    • (3) $\dfrac{m}{M}g\sin\theta\cos\theta$
    • (4) $\dfrac{mg\cos\theta\sin\theta}{M+m\sin^2\theta}$
    • (5) $\dfrac{mg\cos\theta\sin\theta}{M-m\sin^2\theta}$
    • (6) $\dfrac{mg\cos\theta\sin\theta}{M+m\cos^2\theta}$
    • (7) $\dfrac{mg\cos\theta\sin\theta}{M-m\cos^2\theta}$
    • (8) $\dfrac{mg\cos^2\theta}{M+m\cos\theta\sin\theta}$
    • (9) $\dfrac{mg\cos^2\theta}{M-m\cos\theta\sin\theta}$
  • $\fbox{オ}$の解答群
    • (1) $g\sin\theta$
    • (2) $\dfrac{(M+m\cos^2\theta)g\sin\theta}{M}$
    • (3) $\dfrac{(M-m\cos^2\theta)g\sin\theta}{M}$
    • (4) $\dfrac{(M-m)g\sin\theta}{M-m\sin^2\theta}$
    • (5) $\dfrac{(M+m)g\sin\theta}{M+m\sin^2\theta}$
    • (6) $\dfrac{(M-m)g\cos\theta}{M-m\cos^2\theta}$
    • (7) $\dfrac{(M+m)g\cos\theta}{M+m\cos^2\theta}$
    • (8) $\dfrac{(M\sin\theta+m\cos\theta)g}{M+m\cos\theta\sin\theta}$
    • (9) $\dfrac{(M\sin\theta+m\cos\theta)g}{M+m\cos\theta\sin\theta}$
  • $\fbox{カ}$の解答群
    • (1) $mg\cos\theta$
    • (2) $\dfrac{Mmg\cos\theta}{M+m\sin^2\theta}$
    • (3) $\dfrac{Mmg\cos\theta}{M-m\sin^2\theta}$
    • (4) $\dfrac{Mmg\sin\theta}{M+m\cos^2\theta}$
    • (5) $\dfrac{Mmg\sin\theta}{M-m\cos^2\theta}$
    • (6) $\dfrac{Mmg\sin\theta}{M+m\cos\theta\sin\theta}$
    • (7) $\dfrac{Mmg\sin\theta}{M-m\cos\theta\sin\theta}$
    • (8) $\dfrac{mg\cos\theta(M+m\sin^2\theta)}{M}$
    • (9) $\dfrac{mg\cos\theta(M-m\sin^2\theta)}{M}$
• (b) 手を離してから$\text{Q}$が鉛直方向に$h$[m]だけ下がった.床から見た$\text{P}$と$\text{Q}$の水平方向の移動距離をそれぞれ$X$と$x$とすると、$X=\fbox{キ}$、$x=\fbox{ク}$となる。
  このとき、Pの運動エネルギーは$\fbox{ケ}{\times}mgh$と表される。
  • $\fbox{キ}$、$\fbox{ク}$の解答群
    • (1) $\dfrac{Mh}{(M+m)\tan\theta}$
    • (2) $\dfrac{mh}{(M+m)\tan\theta}$
    • (3) $\dfrac{Mh}{(M+m)\sin\theta}$
    • (4) $\dfrac{mh}{(M+m)\sin\theta}$
    • (5) $\dfrac{Mh}{(M+m\cos\theta)\tan\theta}$
    • (6) $\dfrac{mh}{(M+m\cos\theta)\tan\theta}$
    • (7) $\dfrac{Mh}{(M+m\cos^2\theta)\tan\theta}$
    • (8) $\dfrac{mh}{(M+m\cos^2\theta)\tan\theta}$
    • (9) $\dfrac{Mh\sin\theta}{(Msin\theta+m\cos^2\theta)\tan\theta}$
    • (0) $\dfrac{mh\cos\theta}{(Msin\theta+m\cos^2\theta)\tan\theta}$
  • $\fbox{ケ}$の解答群
    • (1) $\dfrac{m}{M+m}$
    • (2) $\dfrac{M}{M+m}$
    • (3) $\dfrac{m\cos^2\theta}{M+m\cos\theta}$
    • (4) $\dfrac{m\cos^2\theta}{M+m\cos^2\theta}$
    • (5) $\dfrac{Mm\cos\theta}{(M+m)(M+m\sin^2\theta)}$
    • (6) $\dfrac{Mm\cos^2\theta}{(M+m)(M+m\sin^2\theta)}$
    • (7) $\dfrac{M^2\cos^2\theta}{(M+m)(M+m\sin^2\theta)}$
    • (8) $\dfrac{Mm\cos^3\theta}{\tan\theta(M\sin\theta+m\cos\theta)(M+m\sin\theta\cos\theta)}$