四角にあてはまる最も適当なものを対応する解答群の中から一つずつ選べ。

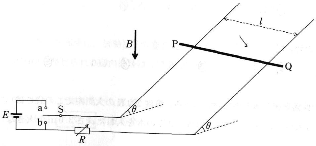
図のように、鉛直下向きで磁束密度の大きさが$B$[T]の一様な磁場中に、2本の平行な導体のレールが傾斜角$\theta$の斜面に沿って固定されている。レールは十分長く、その間隔は$l$[m]である。レールの上に質量$m$[kg]の導体棒$\text{PQ}$をレールと直交する向きにのせる。導体棒はこの向きを保ったままレールの上を運動するものとする。レールの下端には、スイッチ$\text{S}$で切り替えができる、電圧$E$[V]の直流電源と抵抗値$R$[Ω]が可変な抵抗からなる回路が接続されている。可変抵抗以外の導体部分の抵抗および電源の内部抵抗は無視できるものとする。重力加速度の大きさを$g$[m/s²]とする。

• (1) 以下では導体棒$\text{PQ}$とレールの間の摩擦力は無視できるとする。
  • (a) スイッチ$\text{S}$を$a$につなぎ、導体棒に$\text{P}$から$\text{Q}$の向きの電流$I$[A]を流す。このとき、棒$\text{PQ}$が磁場から受ける力の大きさは$\fbox{ア}$[N]である。また、棒$\text{PQ}$がレールから受ける垂直抗力の大きさは$\fbox{イ}$[N]である、棒$\text{PQ}$が速さ$v$[m/s]で動いているとすると、回路に生じる誘導起電力の大きさは$\fbox{ウ}$[V]となる。
  • (b) スイッチ$\text{S}$を$a$につなぎ、棒$\text{PQ}$を手で押さえて抵抗値$R$を調節すると、$R=\fbox{エ}$[Ω]のとき、手を離しても棒$\text{PQ}$は静止したままであった。抵抗値を$R(\lt\fbox{エ})$に固定した後、棒$\text{PQ}$から静かに手を離すと棒は斜面を上昇した。棒の速さが$v$[m/s]のとき、回路を流れる電流の大きさは$I=\fbox{オ}$[A]である。じゅうぶんに時間がたつと棒の速さは一定の値$\fbox{カ}$[m/s]となる。
  • $\fbox{ア}$の解答群
    • (1) $IBl$
    • (2) $IBl\sin\theta$
    • (3) $IBl\cos\theta$
    • (4) $IBl\tan\theta$
  • $\fbox{イ}$の解答群
    • (1) $mg+IBl$
    • (2) $mg\sin\theta+IBl\cos\theta$
    • (3) $mg\cos\theta+IBl\cos\theta$
    • (4) $mg\cos\theta+IBl\sin\theta$
    • (5) $mg\sin\theta+IBl\sin\theta$
    • (6) $mg-IBl$
    • (7) $mg\sin\theta-IBl\cos\theta$
    • (8) $mg\cos\theta-IBl\cos\theta$
    • (9) $mg\cos\theta-IBl\sin\theta$
    • (0) $mg\sin\theta-IBl\sin\theta$
  • $\fbox{ウ}$の解答群
    • (1) $Bv$
    • (2) $Bv\sin\theta$
    • (3) $Bv\cos\theta$
    • (4) $Bv\tan\theta$
    • (5) $Blv$
    • (6) $Blv\sin\theta$
    • (7) $Blv\cos\theta$
    • (8) $Blv\tan\theta$
  • $\fbox{エ}$の解答群
    • (1) $\dfrac{EBl}{mg}$
    • (2) $\dfrac{EBl\tan\theta}{mg}$
    • (3) $\dfrac{EBl}{mg\tan\theta}$
    • (4) $\dfrac{EBl}{mg\sin\theta}$
    • (5) $\dfrac{EBl}{mg\cos\theta}$
    • (6) $\dfrac{EBl\sin\theta}{mg}$
    • (7) $\dfrac{EBl\cos\theta}{mg}$
  • $\fbox{オ}$の解答群
    • (1) $\dfrac{E}{R}$
    • (2) $\dfrac{E+Blv}{R}$
    • (3) $\dfrac{E-Blv}{R}$
    • (4) $\dfrac{E+Blv\sin\theta}{R}$
    • (5) $\dfrac{E-Blv\sin\theta}{R}$
    • (6) $\dfrac{E+Blv\cos\theta}{R}$
    • (7) $\dfrac{E-Blv\cos\theta}{R}$
    • (8) $\dfrac{Blv\sin\theta}{R}$
  • $\fbox{カ}$の解答群
    • (1) $\dfrac{EBl-mgR}{(Bl)^2}$
    • (2) $\dfrac{EBl-mgR\sin\theta}{(Bl)^2}$
    • (3) $\dfrac{EBl-mgR\cos\theta}{(Bl)^2}$
    • (4) $\dfrac{EBl\sin\theta-mgR\cos\theta}{(Bl)^2\cos\theta}$
    • (5) $\dfrac{EBl\sin\theta+mgR\cos\theta}{(Bl\cos\theta)^2}$
    • (6) $\dfrac{EBl\sin\theta-mgR\cos\theta}{(Bl\cos\theta)^2}$
    • (7) $\dfrac{EBl\cos\theta-mgR\sin\theta}{(Bl)^2\cos\theta}$
    • (8) $\dfrac{EBl\cos\theta+mgR\sin\theta}{(Bl\cos\theta)^2}$
    • (9) $\dfrac{EBl\cos\theta-mgR\sin\theta}{(Bl\cos\theta)^2}$
• (2) 以下では導体棒$\text{PQ}$とレールの間の動摩擦係数を$\mu$とする。ただし、$\mu\lt\tan\theta\lt \dfrac{1}{\mu}$とする。
  スイッチ$\text{S}$を$b$につなぎ、棒$\text{PQ}$から静かに手を離すと、棒は斜面を下降し始めた。じゅうぶんに時間がたつと棒の速さは一定の値$\fbox{キ}$[m/s]となる。
  • $\fbox{キ}$の解答群
    • (1) $\dfrac{mgR(\sin\theta-\mu\cos\theta)}{(Bl)^2\cos\theta(\cos\theta-\mu\sin\theta)}$
    • (2) $\dfrac{mgR(\sin\theta+\mu\cos\theta)}{(Bl)^2\cos\theta(\cos\theta-\mu\sin\theta)}$
    • (3) $\dfrac{mgR(\sin\theta-\mu\cos\theta)}{(Bl)^2\cos\theta(\cos\theta+\mu\sin\theta)}$
    • (4) $\dfrac{mgR(\sin\theta+\mu\cos\theta)}{(Bl)^2\cos\theta(\cos\theta+\mu\sin\theta)}$
    • (5) $\dfrac{mgR(\cos\theta-\mu\sin\theta)}{(Bl)^2\cos\theta(\sin\theta-\mu\cos\theta)}$
    • (6) $\dfrac{mgR(\cos\theta+\mu\sin\theta)}{(Bl)^2\cos\theta(\sin\theta-\mu\cos\theta)}$
    • (7) $\dfrac{mgR(\cos\theta-\mu\sin\theta)}{(Bl)^2\cos\theta(\sin\theta+\mu\cos\theta)}$
    • (8) $\dfrac{mgR(\cos\theta+\mu\sin\theta)}{(Bl)^2\cos\theta(\sin\theta+\mu\cos\theta)}$