理想気体である$\text{A}_3\text{B}_6$は、常温付近で、解離して理想気体$\text{AB}_2$を生じ、次のように平衡を保って混合気体になる。

実験1：純粋な理想気体$\text{A}_3\text{B}_6$$n$ molをシリンダーに入れ、温度27℃、圧力$1.0\times10^5$Paの状態に保ち放置した。

実験2：実験1の後、温度27℃に保ったまま、気体の体積が半分になる位置までピストンを移動させた。

• [1] 実験1で$\text{A}_3\text{B}_6$をシリンダーに入れ、十分に時間が経過した後、ピストンの位置は、$\text{A}_3\text{B}_6$を入れた直後と比べてどうなったか。最も適切なものを次の（1）～（3）の中から一つ選べ。$\fbox{ア}$
  • （1）上に移動した
  • （2）下に移動した
  • （3）かわらなかった
• [2] 実験1で十分に時間が経過した後、各物質のモル濃度を$[\text{A}_3\text{B}_6]$、$[\text{AB}_2]$と表すと、濃度平衡定数$K_c$はどう示されるか。最も適切なものを次の（1）～（9）の中から一つ選べ。$\fbox{イ}$
  • （1）$\dfrac{3[\text{AB}_2]}{[\text{A}_3\text{B}_6]}$
  • （2）$\dfrac{27[\text{AB}_2]}{[\text{A}_3\text{B}_6]}$
  • （3）$\dfrac{3[\text{AB}_2]^2}{[\text{A}_3\text{B}_6]}$
  • （4）$\dfrac{[\text{AB}_2]^3}{[\text{A}_3\text{B}_6]}$
  • （5）$\dfrac{9[\text{AB}_2]^3}{[\text{A}_3\text{B}_6]}$
  • （6）$\dfrac{27[\text{A}_3\text{B}_6]}{[\text{AB}_2]}$
  • （7）$\dfrac{3[\text{A}_3\text{B}_6]}{[\text{AB}_2]^2}$
  • （8）$\dfrac{[\text{A}_3\text{B}_6]}{[\text{AB}_2]^3}$
  • （9）$\dfrac{9[\text{A}_3\text{B}_6]}{[\text{AB}_2]^3}$
• [3] 実験1での解離度（分解した割合）を$α(0\leqq a\leqq 1)$、気体の体積を$V$ Lとする。解離度と気体の体積を用いて、濃度平衡定数$K_c$はどのように表せるか。最も適切なものを次の（1）～（9）の中から一つ選べ。$\fbox{ウ}$
  • （1）$\dfrac{6α^3V^2}{1+α}$
  • （2）$\dfrac{9α^3n}{(1+α)V^2}$
  • （3）$\dfrac{3αn}{(1+2α)V}$
  • （4）$\dfrac{27α^3V}{(1+2α)n}$
  • （5）$\dfrac{α^3V}{(1+α)n^2}$
  • （6）$\dfrac{9α}{(1-α)^3nV^2}$
  • （7）$\dfrac{27α^3n^2}{(1-α)V^2}$
  • （8）$\dfrac{3α^2n}{(1-α)V}$
  • （9）$\dfrac{3αV}{(1-2α)^3n^2}$
• [4] 実験1での$\text{A}_3\text{B}_6$の分圧$P_{A3B6}$、$\text{AB}_2$の分圧$P_{AB2}$の値は、αを用いるとどのように表せるか。$\fbox{エ}$、$\fbox{オ}$に最も適切な式を下記のそれぞれの（1）～（9）の中から一つずつ選べ。 \[P_{A3B6}=\fbox{エ}\times10^5\text{Pa}\] \[P_{AB2}=\fbox{オ}\times10^5\text{Pa}\] $\fbox{エ}$
  • （1）$\dfrac{1-α}{α}$
  • （2）$\dfrac{1+2α}{2α}$
  • （3）$\dfrac{1-α}{2α}$
  • （4）$\dfrac{3α}{1-2α}$
  • （5）$\dfrac{α}{1-2α}$
  • （6）$\dfrac{1-α}{1+α}$
  • （7）$\dfrac{1-α}{1+2α}$
  • （8）$\dfrac{α}{1+2α}$
  • （9）$\dfrac{1-2α}{1+2α}$
  $\fbox{オ}$
  • （1）$\dfrac{1+2α}{α}$
  • （2）$\dfrac{1-α}{2α}$
  • （3）$\dfrac{1+α}{2α}$
  • （4）$\dfrac{3α+1}{1-2α}$
  • （5）$\dfrac{α-1}{1-2α}$
  • （6）$\dfrac{2α}{1+α}$
  • （7）$\dfrac{1-2α}{1+2α}$
  • （8）$\dfrac{3α}{1+2α}$
  • （9）$\dfrac{2α-1}{1+2α}$
• [5] 気体反応の場合は、濃度より圧力の方が測定しやすいため、反応に関わる気体の分圧で計算される圧平衡定数$K_p$が用いられる。実験1の圧平衡定数$K_p$はどのように表せるか。最も適切なものを次の（1）～（9）の中から一つ選べ。$\fbox{カ}$
  • （1）$\dfrac{9α^3(1+2α)}{(1-α)^2\times10^{10}}$
  • （2）$\dfrac{9(1+2α)\times10^5}{α(1-α)^2}$
  • （3）$\dfrac{27(1+2α)^2}{α^3(1-α)\times10^5}$
  • （4）$\dfrac{(1+α)(1-2α)^2}{3α^3\times10^{15}}$
  • （5）$\dfrac{(1-α)(1-2α)\times10^{10}}{6α^2}$
  • （6）$\dfrac{(1-α)^3(1+2α)^2\times10^5}{9α}$
  • （7）$\dfrac{3α^3(1-α)\times10^5}{(1+2α)^2}$
  • （8）$\dfrac{9α}{(1-α)(1+2α)^2\times10^{15}}$
  • （9）$\dfrac{27α^3\times10^{10}}{(1-α)(1+2α)^2}$
• [6] 実験2の解離度αの値は実験1と比べてどうなったか。次の（1）～（3）の中から最も適切なものを一つ選べ。$\fbox{キ}$
  • （1）小さくなった
  • （2）大きくなった
  • （3）かわらなった

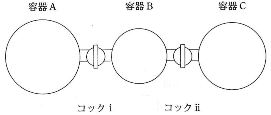
コックⅰとコックⅱを閉じたままで、容器Aにメタンを$9.0\times10^{-2}$mol、容器Bにアルゴンを$4.0\times10^{-2}$mol、容器Cに酸素を$9.0\times10^{-2}$mol封入した。

実験3：コックⅰを開いて、容器Aと容器B内の圧力が一定になるまで放置した。その間、装置全体の温度は27℃に保った。

実験4：実験3のあとコックⅱを開き、全体が一定の圧力になるまで放置した。その後、適切な方法で点火し、反応できる量のメタンを完全燃焼させた。冷却した後、装置全体を27℃に保った。

• [1] 実験3の際のアルゴンの分圧はいくらか。$\fbox{ク}$、$\fbox{ケ}$、$\fbox{サ}$に入る適切な数値をマークし、$\fbox{コ}$には符号を次の（1）と（2）の中から一つ選べ。
  • $\fbox{ク}.\fbox{ケ}\times10^{\fbox{コ}\fbox{サ}}$ Pa
  • 符号
    • $\fbox{コ}$
    • （1）－
    • （2）＋
• [2] 実験4の最後での全圧は何Paか。$\fbox{シ}$、$\fbox{ス}$、$\fbox{ソ}$に入る適切な数値をマークし、$\fbox{セ}$には符号を次の（1）と（2）の中から一つ選べ。
  • $\fbox{シ}.\fbox{ス}\times10^{\fbox{セ}\fbox{ソ}}$ Pa
  • 符号
    • $\fbox{セ}$
    • （1）－
    • （2）＋