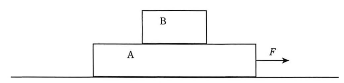
図のように水平な床の上に質量$M$ 〔kg〕の物体Aを置き、その上に質量$m$ 〔kg〕の物体Bを置く、重力加速度の大きさを$g$ 〔$\text{m}$/$\text{s}^2$〕とする。

• (1) 物体Aと物体Bとの間の動摩擦係数を$\mu_1$とし、物体Aと床との間には摩擦力がはたらかないものとする、物体Bを物体Aの右端に置いて静止させた状態から、物体Aに水平方向の瞬間的な力を加えて、物体Aだけに右向きに初速度$v_0$ 〔m/s〕を与えると、最終的には2つの物体はともに一定の速度$v$ 〔m/s〕で運動した。$v=\fbox{ア}$ 〔m/s〕であり、力を加えてから物体Aと物体Bの速度が等しくなるまでの時間は$\fbox{イ}$ 〔s〕となる。ただし、物体Aは十分長く、物体Bは途中で落ちないものとする。

  $\fbox{ア}$の解答群
  • (1) 0
  • (2) $v_0$
  • (3) $\dfrac{m}{M}v_0$
  • (4) $\dfrac{M}{m}v_0$
  • (5) $\dfrac{m}{m+M}v_0$
  • (6) $\dfrac{M}{m+M}v_0$
  $\fbox{イ}$の解答群
  • (1) $\dfrac{v_0}{g}$
  • (2) $\dfrac{Mv_0}{mg}$
  • (3) $\dfrac{mv_0}{Mg}$
  • (4) $\dfrac{v_0}{\mu_1g}$
  • (5) $\dfrac{Mv_0}{\mu_1mg}$
  • (6) $\dfrac{mv_0}{\mu_1(M+m)g}$
  • (7) $\dfrac{Mv_0}{\mu_1(M+m)g}$
  • (8) $\dfrac{mv_0}{\mu_1Mg}$
• (2) 以下の間題では、物体Aと床との間にも摩擦力がはたらくとし、物体Aと床との間の動摩擦係数を$\mu_2$とする。また、物体Aと物体Bとの間の静止摩標係数を$\mu_0(\gt\mu_1)$とする。左の図のように、静止した状態から物体Aを水平方向右向きに大きさ$F$ 〔N〕の力で引いたときの運動を考える。

  • (a) $F=F_0$のとき、物体Aと物体Bは互いに滑らず一体となって連動した。このとき、物体の加速度は$\fbox{ウ}$ 〔$\text{m}$/$\text{s}^2$〕である。

    $\fbox{ウ}$の解答群
    • (1) $\dfrac{F_0}{m+M}$
    • (2) $\dfrac{F_0}{M}$
    • (3) $\dfrac{F_0}{m+M}-\mu_0g$
    • (4) $\dfrac{F_0}{m+M}-\mu_1g$
    • (5) $\dfrac{F_0}{m+M}-\mu_2g$
    • (6) $\dfrac{F_0}{M}-\mu_0g$
    • (7) $\dfrac{F_0}{M}-\mu_1g$
    • (8) $\dfrac{F_0}{M}-\mu_2g$

  • (b) $F$が大きいときは、物体Aと物体Bは別々に動く。物体Aと物体Bが互いに滑らず一体となって運動するときの$F_0$の上限$F_1$は$\fbox{エ}$ 〔N〕である。

    $\fbox{エ}$の解答群
    • (1) $\mu_0(M+m)g$
    • (2) $(\mu_0+\mu_1)Mg$
    • (3) $(\mu_0-\mu_1)Mg$
    • (4) $(\mu_0+\mu_2)Mg$
    • (5) $(\mu_0-\mu_2)Mg$
    • (6) $(\mu_0+\mu_1)(M+m)g$
    • (7) $(\mu_0-\mu_1)(M+m)g$
    • (8) $(\mu_0+\mu_2)(M+m)g$
    • (9) $(\mu_0-\mu_2)(M十m)g$

  • (c) 次に$F=F_2(\gt F_1)$として、静止した状態から力を加えると、物体Aと物体Bは別々に動いた、物体Aから見た物体Bの相対的な加速度は$\fbox{オ}$ 〔$\text{m}$/$\text{s}^2$〕である。

    $\fbox{オ}$の解答群
    • (1) $\mu_1g$
    • (2) $\mu_2g$
    • (3) $\dfrac{F_2}{M}$
    • (4) $(\mu_1+\mu_2)g$
    • (5) $(\mu_1-\mu_2)g$
    • (6) $\dfrac{F_2-\mu_1mg-\mu_2(m+M)g}{M}$
    • (7) $\dfrac{F_2-\mu_1(m+M)g-\mu_2Mg}{M}$
    • (8) $\dfrac{(\mu_2-\mu_1)(m+M)g-F_2}{M}$
    • (9) $\dfrac{(\mu_1+\mu_2)(m+M)g-F_2}{M}$
    • (10) $\dfrac{(\mu_1-\mu_2)(M-m)g-F_2}{M}$