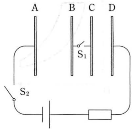
図のように、一辺の長さ$L$の正方形の薄い金属板A、B、C、Dがあり、AB間、BC間、CD間の距離がそれぞれ$2d$、$d$、$d$となるように互いに平行に置かれている。金属板BとCはスイッチ$\text{S}_1$の付いた細い導線で互いに接続されており、金属板AとDはそれぞれスイッチ$\text{S}_2$および抵抗を経由して直流電源に接続されている。

最初、スイッチ$\text{S}_1$と$\text{S}_2$は開いていて。金属板A、B、Dは電荷を持っていないが、 金属板Cには$2Q$ 〔C〕の電荷が与えられている。 $L$ 〔m〕は$d$ 〔m〕よりじゅうぶん大きく、$Q\gt 0$であるとする。 また、金属板間は真空であり、真空の誘電率を$\epsilon_0$ 〔F/m〕とする。

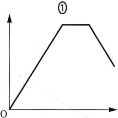
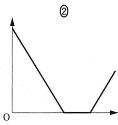
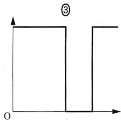
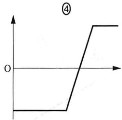
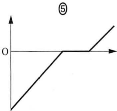
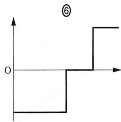
(a) スイッチ$\text{S}_2$は開いたまま$\text{S}_1$を閉じてじゅうぶん時間が経過したとき、金属板AおよびDを貫く電気力線の本数は、 それぞれ$\fbox{ア}$および$\fbox{イ}$であり、極板Aからの距離(AからDに向かう方向を正とする)を横軸、電場(金属板CD間の電場の向きを正とする)を縦軸にとったグラフは$\fbox{ウ}$となる、 、 $\fbox{ア}$、$\fbox{イ}$の解答群
• (1) $\epsilon_0Q$
• (2) $\dfrac{\epsilon_0}{2}Q$
• (3) $2\epsilon_0Q$
• (4) $4\pi\epsilon_0Q$
• (5) $\dfrac{1}{\epsilon_0}Q$
• (6) $\dfrac{1}{2\epsilon_0}Q$
• (7) $\dfrac{2}{\epsilon_0}Q$
• (8) $\dfrac{4\pi}{\epsilon_0}Q$
• (9) 0
$\fbox{ウ}$の解答群






• (b) スイッチ$\text{S}_1$を閉じた後、$\text{S}_2$も閉じてじゅうぶん時間が経過したとき、 金属板AとDにそれぞれ$-3Q$ 〔C〕、$3Q$ 〔C〕の電荷が蓄えられた。このとき、金属板Bが持つ電荷は$\fbox{エ}$ 〔C〕であり、金属板Cが持つ電荷は$\fbox{オ}$ 〔C〕である。また、AB間、BC間、CD間の電場の大きさは、それぞれ$\fbox{カ}$、$\fbox{キ}$、$\fbox{ク}$となる。
  $\fbox{エ}$、$\fbox{オ}$の解答辞
  • (1) $Q$
  • (2) $2Q$
  • (3) $3Q$
  • (4) $4Q$
  • (5) $5Q$
  • (6) $-Q$
  • (7) $-2Q$
  • (8) $-3Q$
  • (9) $-4Q$
  $\fbox{カ}$、$\fbox{キ}$、$\fbox{ク}$の解答群
  • (1) $\dfrac{Q}{2\epsilon_0L^2}$
  • (2) $\dfrac{Q}{\epsilon_0L^2}$
  • (3) $\dfrac{3Q}{2\epsilon_0L^2}$
  • (4) $\dfrac{2Q}{\epsilon_0L^2}$
  • (5) $\dfrac{3Q}{\epsilon_0L^2}$
  • (6) $\dfrac{4Q}{\epsilon_0L^2}$
  • (7) $\dfrac{5Q}{\epsilon_0L^2}$
  • (8) $\dfrac{8Q}{\epsilon_0L^2}$
  • (9) 0
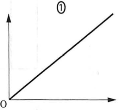
• (c) (b)の問題で、スイッチ$\text{S}_2$を閉じて電荷が蓄えられる過程において、金属板Dの電荷$q(\leqq3Q)$を横軸、Aに対するBの電位$V(q)$を縦軸にとったグラフは$\fbox{ケ}$となる。

  微小な電荷$\Delta q$を金属板AからB、 Cを経由してDまで運ぶのに必要な仕事を考え、Dの電荷が$0$ 〔C〕から$3Q$ 〔C〕となるまでの仕事の総和を求めることにより、金属板が蓄えたエネルギーを求めることができる。スイッチ$\text{S}_2$を閉じる前とくらべて、電荷を蓄えることにより金属板AB間で増加したエネルギーは$\fbox{コ}$となる。
  $\fbox{ケ}$の解答群
  

  
  
  
  
  
  
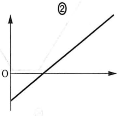
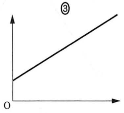
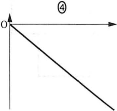
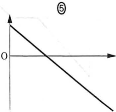  $\fbox{コ}$の解答群
  • (1) $\dfrac{3Q^2d}{2\epsilon_0L^2}$
  • (2) $\dfrac{9Q^2d}{2\epsilon_0L^2}$
  • (3) $\dfrac{15Q^2d}{2\epsilon_0L^2}$
  • (4) $\dfrac{3Q^2d}{\epsilon_0L^2}$
  • (5) $\dfrac{4Q^2d}{\epsilon_0L^2}$
  • (6) $\dfrac{6Q^2d}{\epsilon_0L^2}$
  • (7) $\dfrac{8Q^2d}{\epsilon_0L^2}$
  • (8) $\dfrac{9Q^2d}{\epsilon_0L^2}$
  • (9) $\dfrac{12Q^2d}{\epsilon_0L^2}$
  • (10) $\dfrac{15Q^2d}{\epsilon_0L^2}$