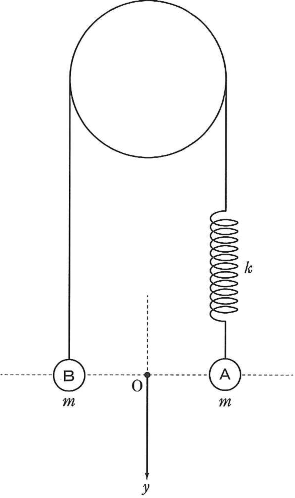
自然長$L$、ばね定数$k$のばねの下端に質量$m$の小球$\text{A}$を付け、ばねの上端はひもを介し、質量$m$の小球$\text{B}$を取り付けた。ここで図のように、水平に固定した円柱にひもをかけたところ、$\text{A}$と$\text{B}$は同じ高さでつり合い、静止した。$y$軸を鉛直下向きにとり、静止したときの小球$\text{A}$、$\text{B}$の$y$座標を$0$とする。ひもと円柱の間の摩擦力は無視でき、ひもは伸ることはなく、ひもとばねの質量は無視できる。重力加速度の大きさは$g$とする。

• 問1 このときのばねの長さは$\fbox{20}$である。
  <$\fbox{20}$の解答群>
  • (1) $L+\dfrac{mg}{2k}$
  • (2) $L+\dfrac{mg}{k}$
  • (3) $L+\dfrac{2mg}{2k}$
  • (4) $L+\dfrac{k}{2mg}$
  • (5) $L+\dfrac{k}{mg}$
  • (6) $L+\dfrac{2k}{mg}$

次に、$\text{A}$と$\text{B}$を$y=0$の位置から鉛直下方に距離$s$だけずらし、同時に静かに放したところ、ひもはたるむことなく、2つの小球は単振動をした。小球を放した時刻を$t=0$として、時刻$t$における$\text{A}$と$\text{B}$の$y$座標をそれぞれ$y_A$、$y_B$、加速度の大きさをそれぞれ$a_A$、$a_B$、ひもの張力の大きさを$T$とする。加速度および力は鉛直下向きを正とする。

• 問2 $\text{A}$の運動方程式は$\fbox{21}$、$\text{B}$の運動方程式は$\fbox{22}$である。
  <$\fbox{21}$の解答群>
  • (1) $ma_A=mg-k(s+y_A+yB)$
  • (2) $ma_A=mg-k(y_A+yB)$
  • (3) $ma_A=mg+k(s+y_A+yB)$
  • (4) $ma_A=mg+k(y_A+yB)$
  • (5) $ma_A=-k(s+y_A+yB)$
  • (6) $ma_A=-k(y_A+yB)$
  • (7) $ma_A=k(s+y_A+yB)$
  • (8) $ma_A=k(y_A+yB)$
  <$\fbox{22}$の解答群>
  • (1) $ma_B=mg-T-k(s+y_A+y_B)$
  • (2) $ma_B=mg-T-k(y_A+y_B)$
  • (3) $ma_B=mg-T-k(2s+y_A+y_B)$
  • (4) $ma_B=T-k(y_A+y_B)$
  • (5) $ma_B=mg-T$
  • (6) $ma_B=T+k(y_A+y_B)$
  • (7) $ma_B=mg+T$
• 問3 時刻$t$におけるばねの長さは$\fbox{23}$である。
  <$\fbox{23}$の解答群>
  • (1) $L+\dfrac{mg}{k}+s\cos\sqrt{\dfrac{k}{m}}t$
  • (2) $L+\dfrac{k}{mg}+s\cos\sqrt{\dfrac{k}{m}}t$
  • (3) $L+\dfrac{mg}{k}+2s\cos\sqrt{\dfrac{k}{m}}t$
  • (4) $L+\dfrac{k}{mg}+2s\cos\sqrt{\dfrac{k}{m}}t$
  • (5) $L+\dfrac{mg}{k}+s\cos\sqrt{\dfrac{2k}{m}}t$
  • (6) $L+\dfrac{k}{mg}+s\cos\sqrt{\dfrac{2k}{m}}t$
  • (7) $L+\dfrac{mg}{k}+2s\cos\sqrt{\dfrac{2k}{m}}t$
  • (8) $L+\dfrac{k}{mg}+2s\cos\sqrt{\dfrac{2k}{m}}t$
• 問4 一方、$s$の値が$\fbox{24}$をこえると、ひもにたるみが生じる。
  <$\fbox{24}$の解答群>
  • (1) $\dfrac{mg}{4k}$
  • (2) $\dfrac{mg}{2k}$
  • (3) $\dfrac{mg}{k}$
  • (4) $\dfrac{2mg}{k}$
  • (5) $\dfrac{k}{4mg}$
  • (6) $\dfrac{k}{2mg}$
  • (7) $\dfrac{k}{mg}$
  • (8) $\dfrac{2k}{mg}$