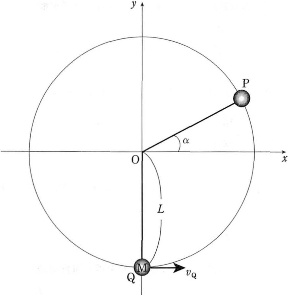
水平方向右向きに$x$軸、鉛直上向きに$y$軸をとる。質量$m$の小球Mを長さ $L$ の糸の下端に付け、糸の上端を原点Oに固定する。Mが最下点Qにあるとき、$x$軸の正の向きに$v_{\text{Q}}$の速度をMに与えた。$v_{\text{Q}}$の値を適切に選び、Mが$x-y$平面上半径 $L$ の円周上を運動し$x$軸を越えた図の点P（∠PO$x$=$\alpha$）で円軌道から離れた後、原点Oを通過するようにした。重力加速度の大きさは$g$とする。MがQP間の円軌道上にあるとき糸と$x$軸のなす角を∠MO$x$=$\theta$とする。ただし、Mの$y$座標が正のときは$\theta$を正とする。

• 問1 MがQP間の円軌道上にあるとき、Mの速さを$v$とする。糸の張力$T$を求めなさい。
  $T=m\left(\fbox{9}+\dfrac{\fbox{10}}{\fbox{11}}\right)$
  [$\fbox{9}$～$\fbox{11}$の解答群]
  • (1) $v$
  • (2) $v^2$
  • (3) $L$
  • (4) $2L$
  • (5) $g\sin\theta$
  • (6) $g\cos\theta$
  • (7) $-g\sin\theta$
  • (8) $-g\cos\theta$
• 問2 $\sin\alpha$を$v_{\text{Q}}$を用いて求めなさい。
  $\sin\alpha=\dfrac{1}{\fbox{12}}\left(\dfrac{\fbox{13}}{\fbox{14}}-\fbox{15}\right)$
• 問3 Mの点Pにおける速さを$v_{\text{P}}$としたとき、${v_{\text{P}}}^2$と${v_{\text{Q}}}^2$の関係を求めなさい。
  ${v_{\text{P}}}^2=\dfrac{1}{\fbox{12}}\left(\fbox{16}-2\fbox{17}\right)$
  [$\fbox{12}$～$\fbox{17}$の解答群]（同じ番号を繰り返し選択可能）
  • (1) 1
  • (2) 2
  • (3) 3
  • (4) 4
  • (5) 5
  • (6) $L$
  • (7) $gL$
  • (8) $v_{\text{Q}}$
  • (9) ${v_{\text{Q}}}^2$
• 問4 Mが点Pから原点Oまで運動する時間$t$を求めなさい。
  $t=\dfrac{1}{v_{\text{P}}}\left(\dfrac{\fbox{18}}{\fbox{19}}\right)$
• 問5 Mが時間$t$の間で運動する鉛直方向の距離と時間の関係を考慮し${v_{\text{P}}}^2$と $\alpha$ の関係式を求めなさい。
  $\fbox{20}\sin\alpha=2\left(v_{\text{P}}\fbox{21}\right)^2$
  [$\fbox{18}$～$\fbox{21}$の解答群]（同じ番号を繰り返し選択可能）
  • (1) $\sin\alpha$
  • (2) $\cos\alpha$
  • (3) $\tan\alpha$
  • (4) $L$
  • (5) $gL$
  • (6) $v_{\text{Q}}$
  • (7) ${v_{\text{P}}}^2$
  • (8) ${v_{\text{Q}}}^2$
• 問6 問2、問3、問5の3式を使って$\tan\alpha$を求めなさい。
  $\tan\alpha=\fbox{22}$
  [$\fbox{22}$の解答群］
  • (1) 1
  • (2) $\dfrac{1}{\sqrt{3}}$
  • (3) $\dfrac{1}{2}$
  • (4) $\dfrac{1}{\sqrt{2}}$
  • (5) 2
  • (6) $\sqrt{2}$
  • (7) 3
  • (8) $\sqrt{3}$