日本大学物理2012年第3問
図1の回路で、$L$ はコイル、$R_1$と $R_2$は抵抗でその値は等しい。$\tilde{E}$は交流電源で、その電圧の時間変化を図2に示す。
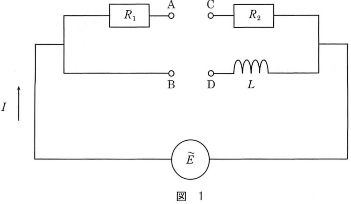
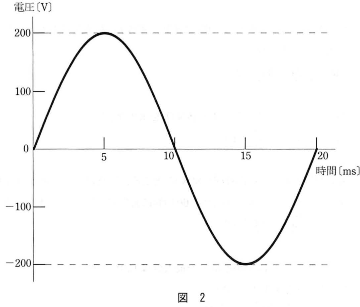


- 問1 交流電源の電圧の実効値$V_{\text{e}}$と角周波数 $\omega$ を求めなさい。
$V_{\text{e}}=\fbox{23}.\fbox{24}\times10^{\fbox{25}}$[V]、$\omega=\fbox{26}\fbox{27}\fbox{28}$[rad/s] - 問2 端子ACをつないだとき、回路に流れた電流 $I$ の最大値は1.25Aであった。抵抗 $R_1$の値を求めなさい。
$R_1=\fbox{29}\fbox{30}$[$\Omega$] - 問3 この回路で60秒間に発生する熱量$Q_1$を求めなさい。
$Q_1=\fbox{31}.\fbox{32}$[$\text{kJ}$] - 問4 端子ACを開き、端子ADをつないだところ、回路に流れた電流の最大値は2.00Aであった。このとき回路で60秒間に発生する熱量$Q_2$を求めなさい。
$Q_2=\fbox{33}.\fbox{34}$[$\text{kJ}$] - 問5 このときコイルにかかる電圧の最大値は120Vであった。コイルの自己インダクタンス $L$ を求めなさい。
$L=\fbox{35}.\fbox{36}\fbox{37}$[H] - 問6 端子ADを開き、端子BDをつないだとき回路に流れる電流が最大となる最初の時刻 $t$ を求めなさい。ただし、このときの電圧の時間変化は図2と同じである。
$t=\fbox{38}\fbox{39}$[ms]