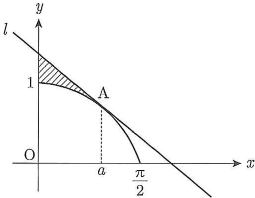
座標平面上に曲線$y=\cos x\left(0\leqq x\leqq\dfrac{\pi}{2}\right)$を描き、この曲線上に点$\text{A}(a,\cos a)$、$\bigg($ただし、$0\lt a\lt \dfrac{\pi}{2}\bigg)$、をとる。この曲線上の点$\text{A}$における接線を$l$とし、曲線と$l$と$y$軸で囲まれる図形（図の斜線部分）の面積を$S(a)$で表す。以下の問いに答えなさい。ただし、(1)、(2)については答えだけを解答欄に書きなさい。

• (1) $S(a)$を求めなさい。
• (2) $\lim\limits_{h\to 0}\dfrac{\cos h-1}{h^2}$を求めなさい。
• (3) $h\gt 0$を$0\lt a-h\lt\dfrac{\pi}{2}$、$0\lt a+h\lt\dfrac{\pi}{2}$を満たすようにとる。つぎの極限値を求めなさい。 \[\lim\limits_{h\to 0}\dfrac{1}{h^2}(S(a+h)+S(a-h)-2S(a))\]