日本医科大学物理2013年第2問

下記の(1)から(3)の文章の四角に適した答えを書きなさい。

(1) 真空中に、2枚の正方形の極板(その一辺は$a$[m])からできている平行板コンデンサーが置かれている。2枚の極板の間隔は$d$[m]である。いま、この2枚の極板の一方に$+Q$[C]、他方に$-Q$[C]の電荷が、それぞれの板上に一様に分布しているとき、2枚の極板間には、単位面積当たり$\fbox{ア}$本の電気力線が存在する。ただし、クーロンの法則における真空中での比例定数を$k$[N・m²/C²]とし、円周率を$\pi$とする。この状態から、2枚の極板の間隔を$d$[m]から$2d$[m]に広げると、2枚の極板間の単位面積当たりの電気力線の本数は、広げる前の$\fbox{イ}$倍である。
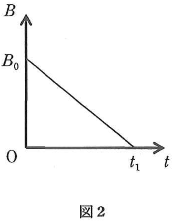
(2) 図1の点$\text{M}$と点$\text{N}$を結ぶ直線(以後これを$\text{MN}$とよぶ)の紙面上、上側には、紙面に垂直で一様な磁束密度$B$[T]が存在している。図1の$\text{MN}$の下側には磁束密度は存在しない。いま、電子1個が、点$\text{M}$において$\text{MN}$に垂直な方向で下側から上側へ通過した。このときの運動量の大きさは$p$[kg・m/s]であった。その後この電子は、点$\text{M}$と点$\text{N}$の中点$\text{O}$を中心とする半円の軌道を描いて点$\text{N}$を通過した。電子の電荷の大きさを$e$[C]とすると、点$\text{M}$と点$\text{N}$の間の長さは$\fbox{ウ}$[m]である。
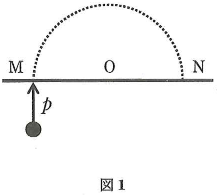
(3) 一辺の長さが$a$[m]の正方形の形状をした3回巻きのコイルが、真空中に置かれていて、磁束密度$B$[T]がコイルの正方形の面に対して常に垂直にかかるようになっている。その磁束密度を、図2のように、$t=0$[s]から$t=t_1$[s]の間に$B=B_0$[T]から$B=0$[T]に直線的に変化させる。

このとき、$t=0$[s]から$t=t_1$[s]の間において、微小時間$\Delta t$[s]の間に変化する磁束の変化量は$\fbox{エ}$[Wb]であり、そのときにコイルに発生する誘導起電力の大きさは$\fbox{オ}$[V]である。