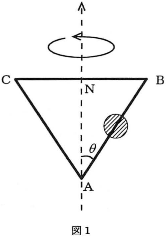
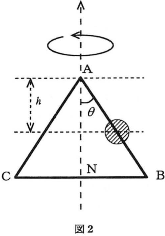
図1、2のように、二等辺三角形状$\left(\overline{\text{AB}}=\overline{\text{AC}}\right)$につながった細い棒に質量$M$［kg］の穴のあいた小球を通し、$\text{BC}$の中点$\text{N}$と$\text{A}$を結ぶ鉛直方向の直線を回転軸として、一定の角速度$\omega$[rad/s]で回転させることを考える。鉛直方向と$\text{AB}$のなす角度を$\theta$[rad]とし、重力加速度を$g$[m/s²]として、下記の文章の四角に適した答えを書きなさい。ただし、距離$\overline{\text{AB}}$は十分長く、小球が$\text{A}$や$\text{B}$の位置に来ることはないものとする。

まず、図1の場合について考える。棒と小球の間に摩擦がないとすると、点$\text{A}$から測った小球の高さが$\fbox{ア}$[m]のときに小球はつり合いの状態にある。また、このとき小球に作用する抗力は$\fbox{イ}$[N]である。

同じく、図1において、$\theta$が$\dfrac{\pi}{4}$[rad]で棒と小球の間に摩擦が作用しているとし、その静止摩擦係数を$\mu$とする。ただし、$\mu$は1より小さい値である。そのとき、小球が滑らずにつり合いを保つためには、点$\text{A}$から測って小球の高さが$\fbox{ウ}$[m]以上、$\fbox{エ}$[m]以下でなければならない。

次に、図2の場合について考える。このときも、棒と小球の間に摩擦が作用するものとする。いま、さまざまな角度$\theta$に対して、$h=1.8\text{m}$の位置に小球を置き、$\omega=7.0\text{rad}/\text{s}$で回転させることを考える。このとき、静止摩擦係数が$\fbox{オ}$以上の場合には、適当な$\theta$でつり合いを保ち続けることができる。ただし、ここでは$g=9.8\text{m}/\text{s}^2$として、有効数字2桁で答えること。