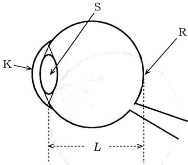
下図は、人の目のモデルを示したものである。正常な目では、物体の明瞭な実像が網膜の上に結ばれ、それを視神経が知覚して、脳に情報を送る。像を結ぶのに必要な光の屈折は、大部分が空気と接している角膜Kの表面で生じるが、筋肉によってレンズの形をした水晶体の焦点距離が変化させられ、物体の明瞭な像が網膜上に結ばれる。水晶体の焦点距離の調節によって、めがねを用いずに明瞭に見える最も遠い点および最も近い点は、それぞれ遠点および近点と呼ばれる。いま、光の進路中における水晶体以外の物質の屈折率は、空気の屈折率と同じと仮定し、また、水晶体を凸レンズと考えて、その焦点距離を$f$[cm]、水晶体の中心点Sと物体の像が結ばれる網膜上の点Rとの距離を$L$[cm]とする。下記の文章の四角に適した答えを有効数字2桁で書きなさい。ただし、$\fbox{エ}$では「近」あるいは「遠」の漢字だけを記入すること。

めがねを用いずに遠方が明瞭に見えて、近点がSから18cm、$L=2.0\text{cm}$のAさんの目について考えてみよう。Aさんが明瞭に物を見る際、筋肉によって水晶体の焦点距離$f$[cm]は変化するが、その最小値は$\fbox{ア}$cmであり、最大値は$\fbox{イ}$cmである。Aさんが、虫めがねを目に非常に近づけて、虫めがねと水晶体の光軸を一致させると、Sから22cmの距離に倍率が3倍の虚像を見ることができるという。この虫めがねの焦点距離は$\fbox{ウ}$cmである。

また、水晶体の調節による焦点距離の最小値と最大値がAさんと同じで、$L=2.2\text{cm}$のBさんがいる。Bさんの目は$\fbox{エ}$視である。

次に、$L=2.0\text{cm}$で、遠点が目から100cmであるCさんの目について考えてみよう。Cさんが遠方を明瞭に見るためにはめがねを必要とするが、そのめがねをSから2.0cm離れた位置に、水晶体と光軸を一致させてかけるものとすると、めがねのレンズの焦点距離は$\fbox{オ}$cmである。