下の図のように、断面積$S$のシリンダーを固定し、なめらかに動く同じ断面積のピストンで$n$モルの理想気体を閉じこめる。ピストンにはばね定数$k$のつる巻きばねがつけられ、その他端は動かない壁に固定されている。はじめ、シリンダー内の気体の体積は$V_0$、シリンダー内外の圧力は$P_0$で、ばねは自然の長さになっている。また、ばねの質量は無視できるものとし、ピストンの質量を$m$、気体定数を$R$とする。下記の文章の四角に適した答えを書きなさい。

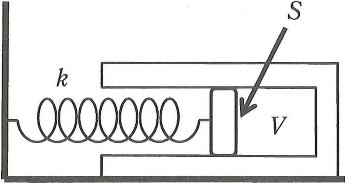
まず、シリンダー内部の気体に熱を加えたところ、シリンダー内部の体積が増えて、ばねは縮み始めた。そのばねの縮みを$x$とすると、気体の圧力は$\fbox{ア}$となる。また、ばねが$L$だけ縮むまでに、シリンダー内部の気体が外部にした仕事は$\fbox{ア}$となる。

次に、シリンダーとピストンを、断熱材で作られた同じ大きさ・形状のものに変え、気体が断熱変化する場合を考える。このとき、気体が温度$T_0$体積$V_0$、圧力$P_0$の状態から、それぞれ微小量$\Delta T$、$\Delta V$、$\Delta P$だけ変化すると、定積モル比熱を$C_V$として、熱力学の第一法則は$\Delta T=\fbox{イ}$のように書ける。また、理想気体の状態方程式$PV=nRT$より、高次の変化量である$\Delta P$と$\Delta V$の積($\Delta P\Delta V$)を無視すると、$P_0\Delta V+V_0\Delta P=nR\Delta T$と書けるので、これと$\Delta T=\fbox{ウ}$を使って、圧力の変化と体積の変化の関係は、$\Delta P=\fbox{エ}$となる。このときにピストンを微小に動かすと、ピストンは単振動を行うが、その単振動の周期は$\fbox{オ}$である。