下記の(1)および(2)の文章の四角に適した答えを書きなさい。ただし、(2)において、理想気体の気体定数を$8.31\text{J}/(\text{mol}\cdot\text{K})$とし、$\fbox{エ}$および$\fbox{オ}$については、有効数字3桁で答えなさい。なお、下図で示されている記号Oは球の中心を示している。

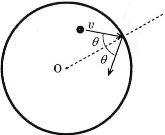
• (1) 半径$r$の球形の変形しない容器に単原子分子の理想気体が入っている。気体分子はすべて同じ質量$m$、同じ速さ$v$をもち、また、気体分子はすべて容器の壁と弾性衝突を行い、気体分子どうしの衝突は無視できるものとする。ある1つの気体分子が、下図に示すように、その入射角を$\theta$として容器の壁に衝突する際、この気体分子の運動量の変化の大きさは$\fbox{ア}$である。この気体分子が単位時間あたり壁に衝突する回数は、$\fbox{イ}$回である。容器の体積を$V$とし、容器内の気体分子の総数を$N$とするとき、気体の圧力は、$m$、$v$、$V$、および$N$だけを用いて表すと$\fbox{ウ}$である。
• (2) 1molの2原子分子理想気体を定圧の条件下で293Kから295Kまで加熱するのに要する熱量は$\fbox{ウ}\text{J}$である。そのうち$\fbox{オ}$%が膨張に使われる。