真空中に一辺の長さが$a$［m］の正方形の領域$\text{PQRS}$があり、正方形の内部には磁束密度$B$$\left[\text{Wb}/\text{m}^2\right]$の一様な磁場がある。磁場の方向は正方形の面(紙面)に垂直で面の裏から表に向いている(図1)。正方形の外部には磁場はない。この磁場に平行に、一辺の長さが$a$の正方形の金属板を図2のように置いた。金属板1の相対する辺の中点は、点$\text{P}$と点$\text{S}$に一致するように、また金属板2の相対する辺の中点は点$\text{Q}$と点$\text{R}$に一致するように置かれ、2枚でコンデンサーを形成している。
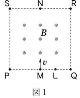
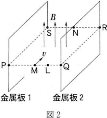磁場のある領域の中へ、質量$m$［kg］、電荷$q$[C]をもつ荷電粒子を速さ$v$[m/s]で入射させたときの運動を考える。粒子は、正方形$\text{PQRS}$が作る平面内で、$\text{PQ}$の中点$\text{M}$から辺$\text{PQ}$に垂直に入射させた。

1. $v=v_1$［m/s]とすると、コンデンサーが帯電していないとき、粒子は点$\text{R}$に到達した。
   • (1)粒子の電荷は正であるか負であるかを記せ。
   • (2)粒子が点$\text{R}$に到達したときの速さ$v_{\text{R}}$[m/s]はいくらか。$v_{\text{R}}$を$a$、$B$、$m$、$q$、$v_1$の中の適当な記号を使って表せ。
   • (3)$v_1$はいくらか。$a$、$B$、$m$、$q$の中の適当な記号を使って表せ。
   次に、金属板1と金属板2の間に電位差$V_1$［V］を与えると、荷電粒子は辺$\text{RS}$の中点$\text{N}$に到達するようになった。（金属板1と金属板2の間の空間には一様な電場が作られると考えてよいものとしよう。）
   • (4)このとき荷電粒子は、領域の中でどのような経路をたどると考えられるか、簡潔に記せ。
   • (5)金属板1と金属板2のどちらの電位が高いか。
   • (6)電位差$V_1$はいくらか。$a$、$B$、$m$、$q$の中の適当な記号を使って表せ。
2. 荷電粒子が磁場の領域に入射するときの速さを$v=v_2$［m/s]に変えると、コンデンサーが帯電していなければ、粒子は$\text{MQ}$の中点$\text{L}$に到達するようになった。
   • (7)点$\text{L}$における粒子の速度の向きを記せ。
   次に、金属板1と金属板2の間に電位差$V_2$［V］を与えると、粒子は辺$\text{RS}$の中点$\text{N}$に到達するようになった。
   • (8)電位差$V_2$は$V_1$の何倍になるか。$\dfrac{V_2}{V_1}$の値を記せ。