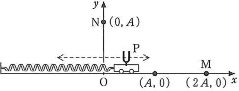
図のように、一端が壁に固定されたバネの他端に、振動数$f_0$[Hz]の音を発しているおんさ$\text{P}$が乗った台車を取り付けて、水平な$xy$平面の$x$軸上を運動するようにこれを設置した。おんさや台車の大きさは無視できる。バネが自然長のときの$\text{P}$の位置を原点$\text{O}(0,~0)$とする。$\text{P}$を原点から$A$[m]離れた位置$(A,~0)$まで手で引いて、時刻$t=0$のときに手を離したところ、$\text{P}$は周期$T$[s]で、$x$軸上を単振動した。空気中の音速を$V$[m/s]とし、$\text{P}$の速さが$V$を上回ることはないものとして、以下の問に答えよ。$\pi$はそのまま残してよい。

$\text{P}$の$x$座標を時刻$t$を用いた式で表すと、$x=A\cos\dfrac{2\pi}{T}t$となる。$\text{P}$の速さの最大値は(1)[m/s]である。

位置$\text{M}(2A,~0)$で音を観測するとき、$\text{P}$が$(A,~0)$の位置で発した音は(2)秒後に$\text{M}$に届き、振動数$(3)\times f_0$の音として聞こえる。観測者が聞く振動数の最大値を$f_{MAX}$[Hz]と表すと、$f_{MAX}=(4)\times f_0$である。この音は$\text{P}$の$x$座標が(5)のときに発した音であり、$\text{M}$に届くまでにかかった時間は(6)秒である。観測者が$f_{MAX}$を聞いてから最初に振動数$f_0$の音を聞くまでの時間は(7)秒である。

次に、位置$\text{N}(0,~A)$で音を観測するとき、$\text{P}$が発した音が$\text{N}$で振動数$f_0$の音として聞こえる$\text{P}$の座標は(8)ヶ所存在する。$\text{P}$の速度を$v_\text{P}$[m/s]、$x$軸の正の向きとベクトル$\overrightarrow{\text{PN}}$のなす角を$\theta$[rad]とすると、$v_\text{P}$の観測者方向への成分は、$v_\text{P}$、$\theta$を用いて(9)と表される。$\text{P}$が位置$\left(\dfrac{A}{2},~0\right)$を原点方向に通過する時に発した音は振動数$(10)\times f_0$として$\text{N}$に届く。