自己インダクタンス$L$[H]の2つのコイル$\text{L}_1$、$\text{L}_2$を近づけておいたときの、2つのコイルの間の相互インダクタンス$M$[H]を測定するために、図のような回路を用意した。抵抗$\text{R}R_1$、$\text{R}_2$、$\text{R}_3$はそれぞれ値$P$[Ω]、$Q$[Ω]、$R$[Ω]の固定抵抗、$\text{R}_4$、$\text{R}_5$は可変抵抗である。また、検流計$\text{G}$の内部抵抗は$r$[Ω]とし、コイル$\text{L}_1$、$\text{L}_2$の抵抗はゼロとする。

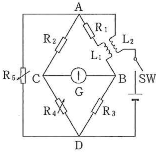
測定は、スイッチ$\text{SW}$を開閉したときも、その後も、検流計の針が常に振れることのないように可変抵抗$\text{R}_4$、$\text{R}_5$を調整して行う。$\text{A}-\text{B}-\text{D}$に流れる電流を$x$[A]、$\text{A}-\text{C}-\text{D}$に流れる電流を$y$[A]、抵抗$\text{R}_5$を流れる電流を$z$[A]とする。また、それぞれの電流の微少時間$\Delta t$の間の変化を$\Delta x$[A]、$\Delta y$[A]、$\Delta z$[A]とする。検流計の針が振れないようにしたときの抵抗$\text{R}_4$、$\text{R}_5$の値は、$S$[Ω]、$W$[Ω]であった。以下の文中の括弧に$P$、$Q$、$R$、$S$、$W$、$r$、$x$、$y$、$z$、$\dfrac{\Delta x}{\Delta t}$、$\dfrac{\Delta y}{\Delta t}$、$\dfrac{\Delta z}{\Delta t}$のうち、適当なものを使った式あるいは等式を記入せよ。なお、10、12、13、14については$P$、$Q$、$R$、$S$、$W$のみを用いて答えよ。

$\text{A}-\text{D}$間の電位差は、$z$を用いて表すと(1)、$y$を用いて表すと(2)である。また、$\text{B}-\text{D}$間の電位差は(3)、$\text{A}-\text{B}$間の電位差$V_{AB}=(4)+L\times (5)+M\times (6)$である。

$\text{SW}$を閉じてから十分時間が経過すると電流は一定値になり、$\text{A}-\text{B}$間の電位差は(7)となる。$\text{A}-\text{B}$間と$\text{A}-\text{C}$間の電位差が等しいことから、等式(8)が成り立ち、また、$\text{B}-\text{D}$間と$\text{C}-\text{D}$間の電位差が等しいことから等式(9)が成り立つ。これらから、$S=(10)$が求まる。

$\text{SW}$を開閉した直後は電流が変化している。$x$、$y$、$z$が変化しているときも検流計の針が振れないためには、$\text{A}-\text{B}$間と$\text{A}-\text{C}$間の電位差が等しくなければならない。すなわち、$V_{AB}=(11)$でなければならない。

また、$\text{B}-\text{D}$間と$\text{C}-\text{D}$間の電位差が等しいことから$y=(12)\times x$であり、また、$\text{A}-\text{B}-\text{D}$間の電位差と$\text{A}-\text{R}_5-\text{D}$間の電位差が等しいことから、$z=(13)\times x$である。従って、$\Delta y$と$\Delta z$を$\Delta x$で表すことができ、$(6)=(14)\times\dfrac{\Delta x}{\Delta t}$となる。以上から$\dfrac{\Delta x}{\Delta t}$がゼロでないときも検流計の針が振れないことから、$M=-L\div(14)$であることがわかる。$L$の前にマイナス符号があるのは、自己誘導による起電力と相互誘導による起電力の向きが逆になっていることを表している。