大阪医科大学物理2013年第4問

以下の問に答えよ。

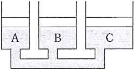
(1) 3本の円筒シリンダー $\text{A}$ 、 $\text{B}$ 、 $\text{C}$ が細管で連結されている。シリンダーの半径はそれぞれ $3.0$ cm、 $4.0$ cm、 $5.0$ cmである。シリンダーに水を入れ、水面には質量が無視できるほど軽い円型ピストンを装着した。ピストンは、シリンダー内の側面と密着しており、かつ滑らかに上下に動くことができる。シリンダー $\text{C}$ のピストンの上に質量 $500$ gのおもりをのせたとき、3つのピストンの高さを等しくするためには、シリンダー $\text{A}$ 、 $\text{B}$ のピストン上にのせるおもりの質量をそれぞれいくらにすればよいか。さらにその後、シリンダー $\text{C}$ のピストンの上に $250$ gのおもりを加えたとき、シリンダー $\text{A}$ 、 $\text{B}$ のピストンはそれぞれ何cm上昇するか。必要ならば、大気圧は $P$ [Pa]、水の密度は $1.0$ g/cm³、円周率は $\pi$ 、重力加速度は $g$ [m/s²]を用いよ。
(2) 容器に水を入れて、上皿はかりでその重さをはかると、 $550$ gであった。球をバネはかりでつるして、この水の中に浸すと、バネはかりの目盛りは $160$ gで、上皿はかりの目盛りは $630$ gになった。球の密度はいくらか。水の密度は1.0g/cm³とする。
(3) 長さ $60$ cm、線密度 $5.0\times 10^{-4}$ kg/mの弦の両端を固定し、張力を $45$ Nかけて振動させると、両端のみを節とする定常波が生じた。この弦の基本振動数はいくらか。なお、この弦を伝わる波の速さ $v$ [m/s]は、張力を $T$ N]、線密度を $\rho$ [kg/m]とすると、 $v=\sqrt{\dfrac{T}{\rho}}$ である。
(4) 極板間の距離を変えられる平行平板コンデンサーがある。このコンデンサーとあるコイルを用いて共振回路を作った。コンデンサーの極板間の距離が $d_0$ [m]のとき、回路の共振周波数が $f_0$ [Hz]であった。コンデンサーの極板間の距離だけを変えることによって、回路の共振周波数を $3f_0$ とするには、コンデンサーの極板間の距離 $d$ [m]をいくらにすればよいか。