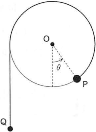
半径$L$［m］の軽い滑車が点$\text{O}$を中心に鉛直面を自由に回転できるようになっている。この滑車の外周上の一点に、質量$2m$［kg］の小さなおもり$\text{P}$を埋め込んで、滑車といっしょに動くようにした。また滑車には軽くて細いひもを介して、質量$m$［kg］のおもり$\text{Q}$を図のようにぶら下げた。ひもの端は$\text{P}$に固定されており、滑車が動くとおもり$\text{Q}$が上下するようになっている。ひもは十分に長く、$\text{Q}$が滑車にぶつかることはない。滑車の質量や摩擦は無視してよいものとする。重力加速度を$g$$\left[\text{m}/\text{s}^2\right]$として、以下の問に答えよ。ただし、滑車の回転角度は$\theta$ radで表し、$\text{P}$が$\text{O}$の鉛直下にあるときを$\theta=0$、反時計回りを正とする。また、$\text{Q}$の運動に関しては、鉛直下方向を正とする。

1. $\theta=0$の状態では、滑車は反時計回りに回転しようとする。滑車が回転しない状態を維持するには、$\text{P}$に対して滑車の接線方向にいくらの力(N)を加えればよいか。
2. 1.の状態から$\text{P}$に加えた力を除くと、$\text{Q}$は下降し始める。動き始めた瞬間の$\text{Q}$の加速度を求めよ。
3. 1.の状態に戻してから、$\text{P}$を手で支えながら滑車をゆっくり動かすと、$0\lt\theta\lt\dfrac{\pi}{2}$の範囲で手の力を必要とせず釣り合う位置がある。このときの角$\theta$の値はいくらか。
   次に、$\theta=\dfrac{\pi}{2}$まで滑車を回転させ、この状態のまま滑車が回転しないように手で止めた。
4. $\theta=\dfrac{\pi}{2}$の時、$\text{Q}$は1.の状態($\theta=0$)よりどれだけ下がっているか。
5. 滑車から手を離すと、滑車は時計回りに回転を始め、$\text{Q}$は上昇を始めた。動き始めた瞬間の$\text{Q}$の加速度を求めよ。
6. 時計回りに回転を始めた滑車は、やがて回転方向が反転する。この反転する位置について正しい記述を選び、記号で答えよ。
   • (ア)　$\theta\gt0$で回転方向が反転する
   • (イ)　$\theta=0$で回転方向が反転する
   • (ウ)　$\theta\lt0$で回転方向が反転する
7. $\text{Q}$は上下に往復運動を繰り返すことになる。この一連の運動の中で$\text{Q}$の速さが示す最大値を求めよ。また、そのときの$\theta$の値はいくらか。