以下の問に答えよ。なお、$\fbox{1}$から$\fbox{5}$については$V$と$\omega$、$\fbox{6}$から$\fbox{8}$については$n$、$m$、$\omega$のうち、必要なものを用いて解答せよ。また、$\fbox{9}$から$\fbox{11}$は$x$、$y$、$z$の等式を、$\fbox{12}$は、$L$、$\rho$、$F$を用いた式を記せ。

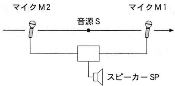
1. 音源$\text{S}$が発する音の振動数$f_0$［Hz］、波長$\lambda$[m]、および音速$V$［m/s］を求めるために観測をした。2個のマイク$\text{M}1$、$\text{M}2$を図のように音源$\text{S}$をはさんで直線上に配置した。そして、2個のマイクで音を検出し、その出力を足し合わせてスピーカー$\text{SP}$を鳴らすようにした。まず、マイク$\text{M}2$を静止させた状態で、マイク$\text{M}1$を音源$\text{S}$から遠ざかるように一定速度$\omega$［m/s］で動かした。$\text{M}1$は、振動数$f=f_0\times\fbox{1}$［Hz］の音を受信する。従って、スピーカー$\text{SP}$からは1秒間に$n=f_0\times\fbox{2}$回のうなりが聞こえる。次に、マイク$\text{M}1$と$\text{M}2$をともに静止させたまま、音源$\text{S}$をマイク$\text{M}1$の方向に速度$\omega$で動かすと、$\text{M}1$は振動数$f_1=f_0\times\fbox{3}$［Hz］の音を受信し、$\text{M}2$は振動数$f_2=f_0\times\fbox{4}$［Hz］の音を受信する。従って、スピーカーからは1秒間に$m=f_0\times\fbox{5}$回のうなりが聞こえる。これらの測定から、音源が出す音の振動数$f_0$は$\fbox{6}$、音速$V$は$\fbox{7}$と求められる。また、波長$\lambda$は、$\fbox{8}$である。
2. 一般に弦の基本振動数$f$［Hz］は、弦の長さ$L$［m］、線密度$\rho$［kg/m］と張力$F$[N]で定まり、 \[f=C\times{L^x}\times\rho^y\times{F^z}\]($C$は次元のない定数) で与えられる。物理量の単位は、時間、長さ、質量の3つの量の組み合わせで決まることを考えれば、上式の両辺について、長さの次元を比較すると$\fbox{9}$という$x$、$y$、$z$が満たすべき式がえられる。また、時間と質量の次元についてもそれぞれ比較して、$\fbox{10}$と$\fbox{11}$という2つの式がえられる。これらの3つの連立方程式を解くと、弦の基本振動数を与える式は \[f=C\times\fbox{12}\] となる。