埼玉医科大学物理2013年第2問

次の文章a、bを読み、下の問い(問1~4)に答えよ。ただし、回路の導線の抵抗は無視できるものとする。また、必要であれば三角関数の加法定理$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$ならびに$x$が十分小さいときの近似式$\cos x\fallingdotseq 1$、$\sin x\fallingdotseq x$を用いよ。

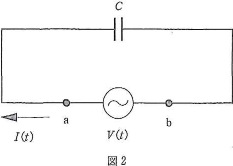
a 図2のように、電気容量$C$のコンデンサーを交流電源に接続した。時刻$t$における、$\text{b}$に対する$\text{a}$の電位を$V(t)$とする。この時刻に電源から$\text{a}$へ向かう電流を$I(t)$、図の左側の極板の電気量を$Q(t)$と記す。キルヒホッフの法則によれば、$\fbox{14}=0$が成り立つ。また、$t$から$t+\Delta t$の間に電気量が$\Delta Q(t)$変化したとすると、$\Delta t$が十分小さければ$\Delta Q(t)=\fbox{15}$と近似できる。この間に電源電圧が$\Delta V(t)$変化したとすると、$\Delta V(t)=\fbox{16}$が成り立つ。一方で$V(t)=V_0\cos(\omega t)(V_0\gt 0、\omega\gt 0)$とすれば、$\Delta V(t)=\fbox{17}$と近似できるから、$I(t)=\fbox{18}$となる。
- 問1
  - (1) $\fbox{14}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $V(t)+Q(t)/C$
    - (b) $V(t)-Q(t)/C$
    - (c) $V(t)+Q(t)$
    - (d) $V(t)-Q(t)$
    - (e) $V(t)+CQ(t)$
    - (f) $V(t)-CQ(t)$
  - (2) $\fbox{15}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $I(t)\Delta t$
    - (b) $-I(t)\Delta t$
    - (c) $V(t)\Delta t$
    - (d) $-V(t)\Delta t$
    - (e) $C\Delta t$
    - (f) $-C\Delta t$
  - (3) $\fbox{16}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $I(t)\Delta t/C$
    - (b) $-I(t)\Delta t/C$
    - (c) $V(t)\Delta t/C$
    - (d) $-V(t)\Delta t/C$
    - (e) $C^2\Delta t$
    - (f) $-C^2\Delta t$
  - (4) $\fbox{17}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $V_0\omega\Delta t\sin(\omega t)$
    - (b) $V_0\omega\Delta t\cos(\omega t)$
    - (c) $-V_0\omega\Delta t\sin(\omega t)$
    - (d) $-V_0\omega\Delta t\cos(\omega t)$
    - (e) $V_0\omega t\sin(\omega \Delta t)$
    - (f) $-V_0\omega t\sin(\omega \Delta t)$
  - (5) $\fbox{18}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $V_0\omega C\sin(\omega t)$
    - (b) $V_0\omega C\cos(\omega t)$
    - (c) $-V_0\omega C\sin(\omega t)$
    - (d) $-V_0\omega C\cos(\omega t)$
    - (e) $\dfrac{V_0\omega Ct\sin(\omega \Delta t)}{\Delta t}$
    - (f) $\dfrac{-V_0\omega Ct\sin(\omega\Delta t)}{\Delta t}$
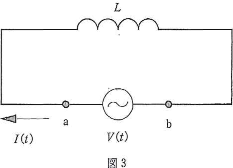
b 次に、図3のように自己インダクタンスが$L$のコイルを同じ交流電源に接続した。$t$から$t+\Delta t$の短時間に電流が$\Delta I(t)$変化したとしよう。キルヒホッフの法則により、$\fbox{19}=0$となる。$V(t)=V_0\cos(\omega t)$と$I(t)$は同じ周期を持つことが期待されるので、$I(t)=I_0\cos(\omega t+\alpha)(I_0\gt 0)$とおいて、$I_0$と$\alpha$を求めてみよう。$\Delta t$が十分小さい時$\Delta I(t)=\fbox{20}$と近似できるから、$V(t)=\fbox{22}$がすべての時刻で成り立つ。従って$I_0=\fbox{22}$、および$\alpha=\fbox{23}$と求めることが出来る。(ただし$-\pi\lt\alpha\leqq\pi$とする。)
- 問2
  - (1) $\fbox{19}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $V(t)+L\dfrac{\Delta I(t)}{\Delta t}$
    - (b) $V(t)-L\dfrac{\Delta I(t)}{\Delta t}$
    - (c) $LV(t)+L\dfrac{\Delta I(t)}{\Delta t}$
    - (d) $LV(t)-L\dfrac{\Delta I(t)}{\Delta t}$
    - (e) $\Delta V(t)-L\Delta I(t)$
    - (f) $\Delta V(t)+L\Delta I(t)$
  - (2) $\fbox{20}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $I_0\omega\Delta t\sin(\omega t+\alpha)$
    - (b) $I_0\omega\Delta t\cos(\omega t+\alpha)$
    - (c) $-I_0(\omega t+\alpha)\sin(\omega\Delta t)$
    - (d) $-I_0(\omega t+\alpha)\cos(\omega\Delta t)$
    - (e) $-I_0\omega\Delta t\sin(\omega t+\alpha)$
    - (f) $-I_0\omega\Delta t\cos(\omega t+\alpha)$
  - (3) $\fbox{21}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $-I_0\omega L\sin(\omega t+\alpha)$
    - (b) $-I_0\omega L\cos(\omega t+\alpha)$
    - (c) $I_0\omega L\sin(\omega t+\alpha)$
    - (d) $I_0\omega L\cos(\omega t+\alpha)$
    - (e) $\dfrac{-I_0(\omega t+\alpha)L\sin(\omega\Delta t)}{\Delta t}$
    - (f) $\dfrac{-I_0(\omega t+\alpha)L\sin(\omega\Delta t)}{\Delta t}$
  - (4) $\fbox{22}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $\dfrac{V_0}{\omega L}$
    - (b) $\dfrac{V_0\omega}{L}$
    - (c) $V_0\omega L$
    - (d) $\dfrac{V_0L}{\omega}$
    - (e) $\dfrac{L\omega}{V_0}$
    - (f) $\dfrac{L}{V_0\omega}$
  - (5) $\fbox{23}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $-\dfrac{1}{2}\pi$
    - (b) $-\dfrac{1}{4}\pi$
    - (c) $0$
    - (d) $\dfrac{1}{4}\pi$
    - (e) $\dfrac{1}{2}\pi$
    - (f) $\pi$
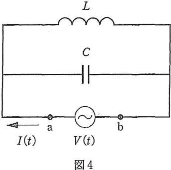
- 問3 問題文a、b中にある素子を用いて図4のような回路を作成した。このとき、電源を流れる電流は$\fbox{24}$である。図4の回路で、$L=1.0\times 10^{-2}$H、$C=4.0\times 10^{-6}$F、$V_0=5.0$Vとしたところ、電源を流れる電流は常に$0$になった。
  - (1) $\fbox{24}$に入る式として最も適切なものを、次の(a)～(h)のうちから1つ選べ。
    - (a) $\left(\omega L-\dfrac{1}{\omega C}\right)V_0\sin(\omega t)$
    - (b) $\left(\omega L-\dfrac{1}{\omega C}\right)V_0\cos(\omega t)$
    - (c) $\left(\dfrac{1}{\omega C}-\omega L\right)V_0\sin(\omega t)$
    - (d) $\left(\dfrac{1}{\omega C}-\omega L\right)V_0\cos(\omega t)$
    - (e) $\left(\omega C-\dfrac{1}{\omega L}\right)V_0\sin(\omega t)$
    - (f) $\left(\omega C-\dfrac{1}{\omega L}\right)V_0\cos(\omega t)$
    - (g) $\left(\dfrac{1}{\omega L}-\omega C\right)V_0\sin(\omega t)$
    - (h) $\left(\dfrac{1}{\omega L}-\omega C\right)V_0\cos(\omega t)$
  - (2) 電源電圧の振動数は$\fbox{25}.\fbox{26}\times 10^{-\fbox{27}}$Hzである。答えは指数表示とし、$\fbox{25}$、$\fbox{26}$、$\fbox{27}$にそれぞれ一の位、小数第1位、指数の数字をマークせよ。ただし、$\fbox{25}\neq 0$とし、数値は枠に合わせて四捨五入せよ。
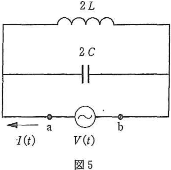
- 問4 図5のように、コンデンサーの容量とコイルの自己インダクタンスをそれぞれ2倍にすると、電源を流れる電流は$\fbox{28}$になった。ただし$I_1\gt 0$とする。
  - (1) $\fbox{ア}$に入る式として最も適切なものを、次の(a)～(f)のうちから1つ選べ。
    - (a) $I_1\cos(\omega t)$
    - (b) $-I_1\cos(\omega t)$
    - (c) $I_1\sin(\omega t)$
    - (d) $-I_1\sin(\omega t)$
    - (e) $I_1{\cos(\omega t)+\sin(\omega t)}$
    - (f) $0$
  - (2) $I_1$の数値は$\fbox{29}.\fbox{30}\times 10^{-\fbox{31}}$Aである。答えは指数表示とし、$\fbox{29}$、$\fbox{30}$、$\fbox{31}$にそれぞれ一の位、小数第1位、指数の数字をマークせよ。ただし、$\fbox{29}\neq 0$とし、数値は枠に合わせて四捨五入せよ。