産業医科大学物理2013年第3問
次の文章を読んで、以下の設間に答えなさい。
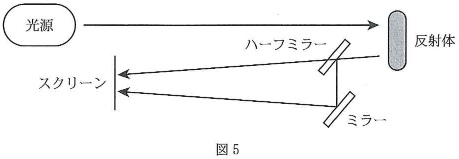
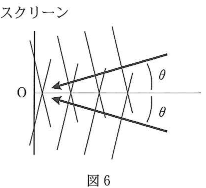
図5のように、光源から出た単一波長$\lambda$[m]のレーザー光が反射体に照射されている。反射体は最初、静止している。反射体からの反射光はハーフミラー(光の一部を透過させ一部を反射する半透明の鏡)によって二つの光路に分けられ、最終的に図6のように同一のスクリーンにその法線に対して反対の方向から同じ角度$\theta$[$^\circ$]で照射される。はじめの状態では、スクリーンの中心$\text{O}$での位相差は$0$である。光路は空気中であり、反射光は平面波とする。


- (1) スクリーン上で二つの光の山と山、谷と谷が干渉して強め合う干渉縞の間隔$l$[m]を$\theta$[$^\circ$]と波長$\lambda$[m]を使って表しなさい。
- (2) スクリーンの中心$\text{O}$での二つの光路の光学的光路差$\Delta$[m]はいくらか。$n$と$L$[m]を使って表しなさい。空気の屈折率は$1$とする。
- (3) このとき、スクリーン上の干渉縞の位置は光学ガラス挿入前とは異なっていた。(2)で求めた光学的光路差$\Delta$が、$\Delta=(i+\delta)\lambda$[m]($i$は整数、$0\leqq\delta 1$)と書けるとき、光学ガラス挿入後の干渉縞の位置は挿入前の位置から見た目でどれだけ移動したか。$\delta$、$\lambda$[m]、$\theta$[$^\circ$]を使って表しなさい。
- (4) (2)で得られた光学的光路差$\Delta$を$\lambda’$を使って表すと、$\Delta=(i+\delta+\delta’)\lambda’$[m]になった。$\delta’$を$\alpha$、$n$、$L$[m]、$\lambda$[m]を使って表しなさい。
- (5) $\alpha=10^{-5}$、$n=1.5$、$\lambda=5\times 10^{-7}$m、$L=5\times 10^{-2}$mのとき、反射体が運動しているときの干渉縞の位置は運動開始前の位置から(1)で求めた干渉縞の間隔$l$[m]のおよそ何倍、移動するか。選択肢(ア)~(エ)から一つ選び、記号で答えなさい。
- (ア) 見た目はほとんど移動しない
- (イ) $l$の0.1倍
- (ウ) $l$の0.2倍
- (エ) $l$の0.5倍
一方の光路に屈折率$n$の光学ガラス(長さ$L$[m])を挿入した(図7)。
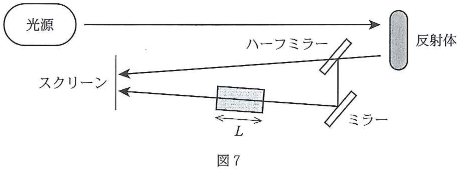
次に、反射体が光源に向かって等速直線運動を始めた(図8)。このとき、反射光の波長が$\lambda’=\dfrac{\lambda}{1+\alpha}$[m]($\alpha$は定数)になった。