産業医科大学物理2013年第1問
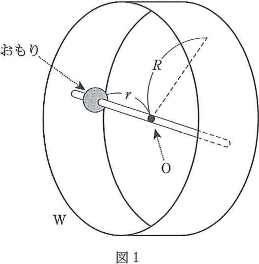
軽い材料で図1のような半径$R$[m]の車輪を作る。この車輪の一つの直径には図1のように直径上の任意の点に留められるようなおもり(質量$m$[kg])が付けられている。車輪およびおもりが取り付けられている棒はおもりに比べて非常に軽いので質量は無視できる。したがって、このおもりの位置がこの装置$\text{W}$の重心の位置である。また、おもりの大きさは$R$に比べて十分小さ いため無視できる。重力加速度を$g$[m/s2]とする。
あらい水平な床にこの装置$\text{W}$が置かれている(図2)。$\text{W}$の中心$\text{O}$を通る水平面と車輪との右側の交点を$\text{A}$とする。おもりと中心$\text{O}$を結ぶ線と線分$\text{OQ}$のなす角を$\theta$[$^\circ$]とする($-180^\circ\lt\theta\leqq180^\circ$:反時計回りを正とする)。はじめ、図2のようにおもりは$R$[m]、$\theta=-30^\circ$に取り付けられている。床と$\text{W}$の静止摩擦係数を$\mu$とする。
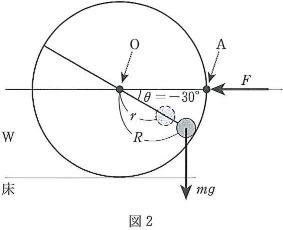
- (1) 点$\text{A}$に水平方向左向きの力$F$[N]を作用させる。$\text{W}$がすべらないための条件を、$F$[N]、$m$[kg]、$g$[m/s2]、$\mu$を用いて表しなさい。
- (2) $\text{W}$がすべらずにつり合って静止しているとき、$F$[N]の大きさを与えられた記号を用いて表しなさい。
- (3) 8を固定したまま中心から$r$[m]におもりを移動させ、点$\text{A}$に水平方向左向きの力$F’$[N]を作用させた。$\text{W}$はすべらず、つり合った状態で静止した。$F’$[N]の大きさを与えられた記号で表しなさい。
- (4) 斜面と$\text{W}$の静止摩擦係数を$\mu’$とする。$\text{W}$がすべらないための条件を$\mu’$と$\alpha$[$^\circ$]を用いて表しなさい。
- (5) 中心$\text{O}$から$r$[m]、任意の角度$\theta$[$^\circ$]におもりがあるとき、$\text{W}$にはたらく力のモーメントの総和$N$[N・m]を与えられた記号で表しなさい(左回り(反時計回り)を正とする)。
- (6) おもりの位置が$r=R$[m]の時、支えなしに$\text{W}$が斜面上で右にも左にも回転せず静止する$\theta$[$^\circ$]の値が二つある。大きい方をz$\theta_1$[$^\circ$]、小さい方を$\theta_2$[$^\circ$]とするとき、それぞれを$a$[$^\circ$]を使って表しなさい。
- (7) どんな$\theta$でも$N$[N・m]が正になる$r$[m]の条件を求めなさい。
次に、図3のように、この装置$\text{W}$を角度$\alpha$[$^\circ$]$(0^\circ<\alpha<90^\circ)$のあらい斜面に置く。$\text{W}$の中心$\text{O}$を通る水平面と車輪との右側の交点を$\text{A}$とする。おもりと中心0を結ぶ線と線分$\text{OA}$のなす角を$\theta$[$^\circ$]とする($-180^\circ\lt\theta\leqq180^\circ$:反時計回りを正とする)。
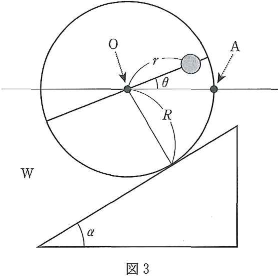
以下では(4)の条件が常に満たされており、角度\alpha[°]の斜面上で$\text{W}$はすべらないものとする。