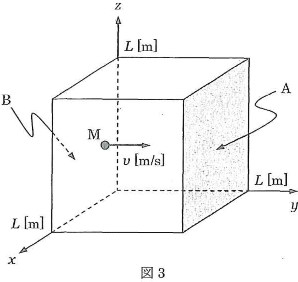
単原子分子理想気体が図3のように一辺の長さ$L$[m]の立方体に閉じこめられている。この理想気体分子のうち、壁$\text{A}$に垂直に向かう速さ$v$[m/s]をもつ1個の分子$\text{M}$を考え、この$\text{M}$が壁$\text{A}$に完全弾性衝突したとする。$\text{M}$の質量を$m$[kg]としたとき、$\text{M}$の衝突前後の運動量の変化の大きさは(1)[kg・m/s]である。$\text{M}$はその後、壁$\text{A}$と平行な壁$\text{B}$に向かい、壁$\text{B}$ と完全弾性衝突後にふたたび壁$\text{A}$へ向かうという往復運動を行う。$\text{M}$が壁$\text{A}$と衝突する回数は毎秒(2)回となるため、$\text{M}$が壁$\text{A}$から1秒あたりに受ける運動量の変化の大きさは(3)[kg・m/s²]である。

実際の分子の速度ベクトルは大きさも方向もさまざまだが、方向によって条件は変わらないので、各壁に対して垂直な速度成分を考えれば、衝突する壁による分子の運動量の変化のしかたに違いはない。そのため立方体中の全分子の運動量の変化は、全分子の(4)ずつがそれぞれの速さで図3の$x$、$y$、$z$の各軸に平行に運動している場合に等しい。

さて、立方体中の分子の総数$N$をきわめて大きな数とすると、これらの分子が壁$\text{A}$に$1$秒あたりに衝突する回数はほとんど変動せず一定であると考えられる。そのため、各分子の速さの$2$乗を平均したものを$\overline{v^2}$[m²/s²]とすると、壁$\text{A}$が1秒あたりに分子に与える運動量の変化の総和の大きさは(5)[kg・m/s²]となる。

単位時間あたりに物体が受ける運動量の変化は物体の受ける外力に等しいため、壁$\text{A}$が$1$秒あたりに分子に与える運動量の変化の総和は壁$\text{A}$が分子に及ぼす力の総和であり、これはその反作用として気体分子が壁$\text{A}$に及ぼす力の総和を与える。

次に、気体分子が壁$\text{A}$に及ぼす単位面積あたりの力、つまり圧力を考えよう。壁$\text{A}$の面積は(6)[m²]であり、この立方体内の気体の体積$V$は(7)[m³]なので、$V$を用いると壁$\text{A}$には(8)[Pa]の圧力が生じている。式(8)では分子が閉じこめられている領域の$x$、$y$、$z$方向の長さが消え、もはや領域の大きさや形によらないものとなっている。

最後に、この立方体内部について、気体の圧力$P$[Pa]が一定の場合にその体積$V$[m³]が絶対温度$T$[K]に比例するというシャルルの法則を考える。この法則は、比例定数を$k$[m³/K]と置けば \[V=kT\] と書けるので、これを(8)に当てはめると \[T=(9)\] となり、$P$が一定という条件なら$T$は(10)にのみ影響を受けることが導かれる。