図3(a)のように屈折率1の空気中から屈折率1.3の薄い石鹸の膜に入射角30度で白色光を入射し、その屈折率をプリズムに通したら虹が観察された。その虹を肉眼で観察したところ暗線が1本確認でき、その暗線の波長は0.66 $\mu$m$($ただし$\mu=10^{-6})$であった。これらの観測から以下の考察によって薄い膜の厚さ$d$を求めよう。以下の考察において、〔 〕 に当てはまる記号、または数値を答えなさい。数値は分数を使っても良い。必要なら図3(b)を用いなさい。

図3(a)中の(ア)の経路の光と(イ)の経路の光が干渉したとする。また、(イ)の経路において入射角を$i$、屈折角を$j$、とする。暗線が生じる条件は

「光路長の差$=m\lambda~(m=1,2,3,\cdots)$、ただし$\lambda$は干渉現象により生じた暗線の波長」

である。まずは光路長の差を求めよう。ここで、光路長とは、光の進む距離を真空中で進む距離に換算した量のことである。たとえば光が屈折率$n$の媒質中を$L$だけ進んだとすると、真空中では同じ時間内で〔 1 〕だけ進む。このとき$L$を幾何学的距離、〔 1 〕を光路長という。図3(a)中の(ア)の経路と(イ)の経路との幾何学的距離の差は図3(a)中の太線で示されている。したがって、膜の屈折率を$n$とすると、光路長の差は$d$、$n$、$j$を用いて〔 2 〕と表せる。屈折の法則より$i$、$j$、$n$の関係は$n=$〔 3 〕であり、$n=1.3$、$i=30$度を代入すると$\cos j$、は〔 4 〕と書ける。以上より、膜の厚さ$d$、暗線の波長$\lambda$、および$m~(m=1,2,3,\cdots)$を用いて〔 5 〕と書ける。

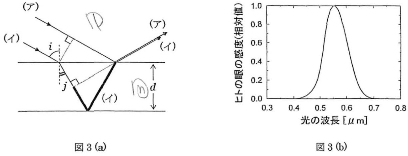
観察された暗線が$m=1$に対応すると仮定すると、肉眼で確認できる暗線の波長は0.66 $\mu$mの1本のみである。観察された暗線が$m=2$に対応すると仮定すると、肉眼で確認できる暗線の波長は0.66 $\mu$mおよび〔 6 〕$\mu$mの2本であり、観察結果と異なることになる。観察された暗線が$m=3$に対応すると仮定すると肉眼で確認できる暗線の数は〔 7 〕本となる。$m=1,2,3$を計算してみると$m=3$以降の考察は必要ないことがわかる。以上の考察より、膜の厚さは〔 8 〕$\mu$mである。