• (1) 跳ね上がった後にボールが達する最高点は、床からどれだけの距離にあるか。$h$、$e$、$g$の中から必要なものを用いて表しなさい。
• (2) ボールはその後、落下と上昇を繰り返して、最後に床に静止した。最初の高さから静止するまでにポールが移動した距離はいくらか。$h$、$e$、$g$の中から必要なものを用いて表しなさい。

$\fbox{B}$ 長さ$30$cm程度のごく細い棒がある。その重心は長さ方向の中心からずれている。その重心を、摩擦の特性を使って見つける次のような方法がある。

平行にした両手の人差し指に、棒の両端を直交するように載せて棒を水平に保つ。棒を水平に保ったまま両人差し指を互いに近づける。すると重心からより遠い人差し指（これをいま左手の人差し指$\text{L}$とする）の方が滑り始め、他方（右手）の人差し指$\text{R}$は静止したままである。その後、滑っていた$\text{L}$が止まり、それまで静止していた$\text{R}$が$\text{L}$の方向に滑り始める。これが交互に繰り返され、両手の人差し指$\text{L}$とRが一緒になった点が棒の重心である（指の太さがごく細いものと仮定する）。なぜならその点で棒を支えることができるからである。

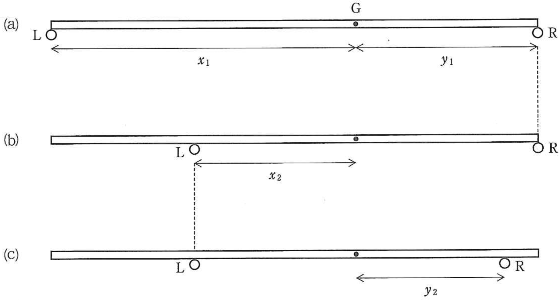
図を使って説明しよう。図(a)に、最終的に見いだされる重心$\text{G}$と棒の両端に$\text{L}$と$\text{R}$を添えた状態を示す。重心と$\text{L}$、重心と$\text{R}$の間の距離をそれぞれ、$x_1$と$y_1$とする。最初$\text{L}$が滑り始めた。図(b)のように$\text{GL}=x_2$になったところで、$\text{L}$は止まり$\text{R}$が滑りはじめた。そして図(c)のように、$\text{GR}=y_2$となったところで、$\text{R}$は止まり$\text{L}$が滑りはじめた。

図(b)のように、$\text{GL}=x_2$、$\text{GR}=y_1$になったとき、$\text{L}$から棒に働く垂直抗力の大きさを$A(x_2,y_1)$と置き、$\text{R}$から棒に働く垂直抗力の大きさを$B(x_2,y_1)$と置く。棒の重さ（棒の質量と重力加速度の積）を$W$とする。なお、棒と両人差し指$\text{L}$、$\text{R}$との間の静止摩擦係数と動摩擦係数をそれぞれ$\mu$、$\mu’$とする。

• (1) $A(x_2,y_1)$と$B(x_2,y_1)$をそれぞれ$x_2$、$y_1$、$W$を使って表しなさい。
• (2) 図(a)の状態から図(b)の状態に移る際、G$\text{L}$がまさに%2になって$\text{L}$が止まろうとして、$\text{R}$がまさに滑り始めようとしたとき$\mu$、$\mu’$、$A(x_2,y_1)$、$B(x_2,y_1)$の間にどのような関係が成り立つか。
• (3) 図(b)で、重心$\text{G}$の位置は線分$\text{LR}$を$\alpha:1$に内分する。$\alpha$はどのように表されるか。$\mu$、$\mu’$を用いて表わしなさい。
• (4) 上に述べた操作が、理論上無限に繰り返されて$\text{L}$と$\text{R}$が$\text{G}$に到達したとする。このとき$\sum\limits_{k=1}^\infty y_k$を、$\mu$、$\mu’$および$y_1$を使って求めよ。