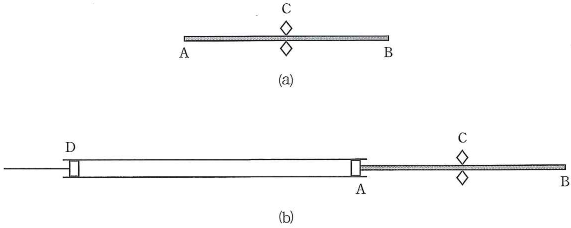
図(a)に示すように、長さ$L$の金属棒$\text{AB}$の中点$\text{C}$を固定し、長さ方向に摩擦すると、金属棒中に$\fbox{1}$波を起こすことができる。この$\fbox{1}$波は基本振動であった。すなわち固定した部分$\text{C}$は波の$\fbox{2}$、金属棒の両端$\text{A}$と$\text{B}$が波の$\fbox{3}$となった。$\fbox{1}$波の伝わる速さ$V$は金属棒のヤング率とよばれる物理量$E$、および金属棒の密度$\rho$と次の関係にあることがわかっている。 \[V=\sqrt{\dfrac{E}{\rho}}\tag{K}\label{aa}\] 逆に、金属棒を伝わる一波の速さがわかれば金属棒のヤング率が得られる。

この速さ$V$を求めるために長さ$1.5$mあまりのガラス管を用意した。図(b)に示すようにガラス管の一端はコルクのせん$\text{D}$でふさぐ。金属棒$\text{AB}$の$\text{A}$にコルクのせんを取り付けガラス管の他端に差し込んだ。金属棒とガラス管は一直線をなしていて、ともに水平に保たれている。また、金属棒の中点$\text{C}$は固定してある。

コルク$\text{D}$の位置を変えることにより密閉ガラス管内の気柱の長さを変えることができる。このようにして、密閉ガラス管中の気柱をある長さに変えると、金属棒に生じた$\fbox{1}$波を密閉ガラス管の中に$\fbox{4}$させることができる。すなわち、密閉ガラス管の中（の空気中）に音波の$\fbox{5}$波を発生させることができる。実際、あらかじめガラス管の中に軽い粉末を封入しておくと、$\fbox{4}$によって粉末がしま模様を作る。このしま模様の間隔から音波の波長を調べると、$\fbox{4}$振動数がわかる。

• (1) 式$\eqref{aa}$の両辺にある物理量の単位に注目することで、ヤング率$E$の次元がわかる。ヤング率$E$の次元は、どのような物理量と同じか。その物理量を(たとえば、『力』というように)挙げなさい。
• (2) 密閉ガラス管中にできたしま模様の間隔が$0.100$mであった。密閉ガラス管中に発生した音波の振動数はいくらか。
• (3) 金属棒の長さが$1.00$mであった。金属棒に発生した$\fbox{1}$波の伝わる速さはいくらか。
• (4) 金属棒の密度は$9.00$g/cm³であった。この金属棒のヤング率はいくらか。単位に気をつけなさい。