昭和大学物理2012年第2問
以下の問題で、大気圧と温度は変化しないものとする。
- [ A ]
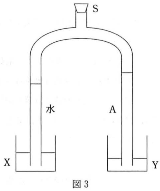
(1) 静止流体がある(図1)。流体中の1と2における圧力がそれぞれ$p_1$と$p_2$であった。これらの位置は容器の底面からそれぞれ$h_1$、$h_2$の高さにある。流体の密度を$d$、重力加速度の大きさを$g$としたとき$p_1$、$p_2$の間の関係式を書き下しなさい。
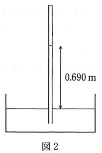
以下の問題で水の密度は1.00 g/cm3、水銀の密度は水の密度の13.6倍としなさい。- (2) 昭和大学・富士吉田校舎は富士山のすそ野にある。この場所で、およそ1mほどの長さの試験管を用意し、それに水銀をめいっばい詰め、試験管の口を閉じて水銀の入った容器に逆さにして垂直に立てた。その後静かに試験管の口を開けると試験管内の液面が下がった(図2)。容器内の液面と試験管内の液面の高さの差(すなわち水銀柱の高さ)が0.690 mであった、この場所における重力加速度の大きさが9.80 m/s2としたとき。この場所の大気圧は何Paか。
- (3) 上と同じ場所で、水銀の代わりに水を用いて上と同様な装置(ただし試験管は充分に長いもの)を使って大気圧を測るとしたら、水柱の高さはいくらとなるか。
- (4) 血圧を水銀血圧計で測ってくれた医師に、最高血圧が110と言われた。これは何Paのことか。
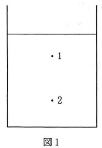
- [ B ] 図3に示す装置を使って、液体Aの密度を以下のようにして測ることにしよう。
内径の一様なガラス管をU字型に曲げ、その中央に栓Sを備えた側管を取り付け、これを図3に示すように逆さに立ててガラス管が垂直になるように固定する。ガラス管の両端の開口部に、管に比べてかなり大きめの全く同型の容器XとYを差し込む。容器Xに密度のわかっている水を入れ、容器Yに密度の未知な液体Aを入れる。その後栓Sを通してガラス管内の空気を吸い上げる。すると管内にそれぞれの液体が吸い上げられる。両方の液体が混ざらないように注意する。2本のガラス管にはそれぞれ長さ方向に目盛りが付けてある。以下では左右にあるガラス管内の液面と、容器内の液面の位置(高さ)を、それぞれのガラス管に付いている目盛りで読む。なお毛細管現象などは考えない。
今左側ガラス管内の水の液面が示す高さが$a_1$で、容器Xの液面が示す高さが$a_1'$であった。同様に右側ガラス管内の液体Aの液面が示す高さが$b_1$で、容器Yの液面が示す高さが$b_1'$であった。
- (1) 管内の空気の圧力が$p_1$である時、大気圧を水の密度$\rho$、$a_1$、$a_1'$および$g$を使って表しなさい。
- (2) $a_1$、$a_1'$、$a_2$、$a_2'$、$b_1$、$b_1'$、$b_2$、$b_2'$の間に成り立つ関係式を一つ示しなさい。
- (3) 液体Aの密度を$\rho$、$a_1$、$a_2$、$b_1$、$b_2$を使って表しなさい。
