ベータトロンは真空中に発生させた誘導電界を利用して電子を同一円軌道上で加速する装置である。この装置の原理は以下のようなものである。

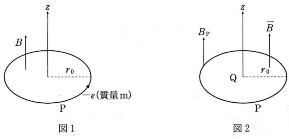
$z$軸の正方向を向いた、大きさ$B$の一様な磁束密度の中で、電荷$-e(\lt0)$、質量$m$を持つ電子が、$z$軸を中心とする$x-y$平面で半径$r_0$の等速円運動を行っている(図1)。この円軌道をPとする。このとき以下の問いに答えなさい。「計算」欄に計算も記しなさい。

• (1) 電子の連動方向は$z$軸の正方向から見て、時計回りか、あるいは反時計回りか。
• (2) 電子の速さを$e$、$m$、$r_0$、$B$を用いて表しなさい。

次に図2のように、磁束密度の大きさが時間と$z$軸からの距離にのみ依存して変わるような場合を考える。

• (3) このとき円軌道Pで囲まれる面Qを貫く磁束密度の平均の大きさが$\bar{B}$であるとしたら、この円軌道面Q内の平均の磁束はいくらか。
• (4) $\bar{B}$を時間$\Delta t$の間に$\Delta\bar{B}$の割合で増やした。その結果円軌道Pにどれだけの大きさの誘導起電力が生じたか。またこれによって、電子に生じる軌道の接線方向の加速度の大きさ$\dfrac{\Delta v}{\Delta t}$はいくらとなるか。なお$\Delta v$は$\Delta t$の間の速さの変化である。
• (5) 速度が上昇している電子を、同じ軌道P上で運動させておくためには、軌道P上の磁束密度$B_\text{p}$の時間変化$\dfrac{\Delta B_\text{P}}{\Delta t}$は。面Qを貫く磁束密度の平均$\bar{B}$の時間変化$\dfrac{\Delta \bar{B}}{\Delta t}$とどのような関係にあればよいか。