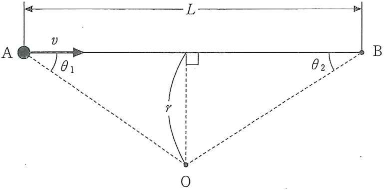
一定の速さ$v$で直線上を進んでいる振動数$f$の音源がある。図のように、直線から$r$だけ離れた点$\text{O}$でその音を観測する。音源の運動する直線上にある点$\text{A}$と点$\text{B}$の間の距離を$L$、直線$\text{AB}$と直線$\text{AO}$のなす角を$\theta_1$、直線$\text{AB}$と直線$\text{BO}$のなす角を$\theta_2$とする。音源の速さ$v$は音速$V$よりも遅いとして、以下の問13から問15に答えよ。

• 問13 点$\text{A}$で出た音が点$\text{O}$で観測されるときの振動数はいくらか。
  • (a) $\dfrac{V}{V-v\cos\theta_1}f$
  • (b) $\dfrac{V}{V+v\cos\theta_1}f$
  • (c) $\dfrac{V-v\cos\theta_1}{V}f$
  • (d) $\dfrac{V+v\cos\theta_1}{V}f$
  • (e) $\dfrac{V+v\cos\theta_1}{V-v\cos\theta_1}f$
  • (f) $\dfrac{V-v\cos\theta_1}{V+v\cos\theta_1}f$
• 問14 点$\text{A}$と点$\text{B}$がはるか遠方のときは、$\theta_1=\theta_2=0$とみなせる。このとき、点$\text{A}$で出た音の点$\text{O}$で観測された振動数は、点$\text{B}$で出た音の点$\text{O}$で観測された振動数の2倍であった。音源の速さ$v$はいくらか。
  • (a) $v=\dfrac{V}{4}$
  • (b) $v=\dfrac{V}{3}$
  • (c) $v=\dfrac{V}{2}$
  • (d) $v=\dfrac{2}{3}V$
  • (e) $v=\dfrac{3}{4}V$
• 問15 音源が点$\text{A}$から点$\text{B}$までの間だけ音を出したものとすると、点$\text{O}$では何秒間だけ音が聞こえるか。
  • (a) $\dfrac{L}{v}+\dfrac{r}{V}\dfrac{\cos\theta_1-\cos\theta_2}{\cos\theta_1\cos\theta_2}$
  • (b) $\dfrac{L}{v}+\dfrac{r}{V}\dfrac{\cos\theta_1+\cos\theta_2}{\cos\theta_1\cos\theta_2}$
  • (c) $\dfrac{L}{v}+ \dfrac{r}{V} \dfrac{\cos\theta_2-\cos\theta_1}{\cos\theta_1\cos\theta_2}$
  • (d) $\dfrac{L}{v}+\dfrac{r}{V}\dfrac{\sin\theta_1-\sin\theta_2}{\sin\theta_1\sin\theta_2}$
  • (e) $\dfrac{L}{v}+\dfrac{r}{V}\dfrac{\sin\theta_1+\sin\theta_2}{\sin\theta_1\sin\theta_2}$
  • (f) $\dfrac{L}{v}+\dfrac{r}{V}\dfrac{\sin\theta_2-\sin\theta_1}{\sin\theta_1\sin\theta_2}$