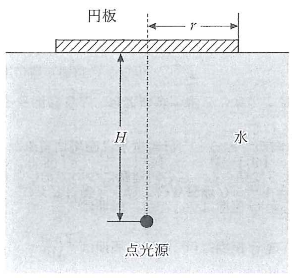
問19 図のように、水面から深さ$H$の水中に点光源を置いた。点光源の真上の水面に半径$r$の不透明な円板を浮かべて、上方の空気中のどこから見ても点光源が見えないようにしたい。円板の最小の半径はいくらか。ただし、空気の屈折率を$1$、水の屈折率を$n$とする。また、円板の厚さは無視できるとする。

• (a) $\dfrac{H}{\sqrt{n^2-1}}$
• (b) $\dfrac{H}{\sqrt{n-1}}$
• (c) $\dfrac{H}{n^2-1}$
• (d) $\dfrac{H}{2\sqrt{n^2-1}}$
• (e) $\dfrac{H}{2\sqrt{n-1}}$