東邦大学物理2012年第1問

次の問1から問5に答えよ。

問1 静止したエレペー夕の天井から単振子をさげ、振動の周期を測ったら$T_1$であった。エレベータが上向きに加速度運動をしているとき、この単振子の周期は$T_2$であった。エレペー夕の加速度はいくらか。重力加速度の大きさを$g$とする。
- a. $\bigg\{\bigg(\dfrac{T_1}{T_2}\bigg)^2+1\bigg\}g$
- b. $\bigg\{\bigg(\dfrac{T_1}{T_2}\bigg)^2-1\bigg\}g$
- c. $\bigg\{\bigg(\dfrac{T_2}{T_1}\bigg)^2+1\bigg\}g$
- d. $\bigg\{\bigg(\dfrac{T_2}{T_1}\bigg)^2-1\bigg\}g$
- e. $\bigg\{\dfrac{T_2}{T_1}+1\bigg\}g$
- f. $\bigg\{\dfrac{T_1}{T_2}-1\bigg\}g$
問2 500 Wの電気ポットに0℃、500 gの氷がはいっている。100℃のお湯にするには電気ポットに何秒間電流を流せばよいか。ただし、水の比熱は4.2 J/g.K、融解熱は330 J/gである。また、熱は外部に逃げないものとする。
- a. 330s
- b. 420s
- c. 500s
- d. 750s
- e. 1100s
- f. 1200s
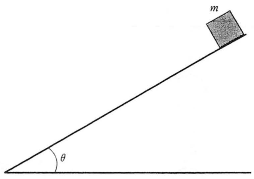
問3 水平な床の上に板があり、この板の端に質量$m$の小さな物体が置いてある。物体が置いてあるほうを持ち上げたところ、板と床の間の角度が$\theta$になったところで物体が滑り始めた。動庫標係数を$\mu$とすると、物体が板にそって長さ$L$だけすべるのに必要な時間はいくらか。ただし、角度$\theta$は保たれていて、重力加速度の大きさを$g$とする。
- a. $\sqrt{\dfrac{L}{g(\sin\theta-\mu\cos\theta)}}$
- b. $\sqrt{\dfrac{L}{g(\sin\theta+\mu\cos\theta)}}$
- c. $\sqrt{\dfrac{2L}{g(\sin\theta-\mu\cos\theta)}}$
- d. $\sqrt{\dfrac{2L}{g(\sin\theta+\mu\cos\theta)}}$
- e. $\sqrt{\dfrac{3L}{g(\sin\theta-\mu\cos\theta)}}$
- f. $\sqrt{\dfrac{3L}{g(\sin\theta+\mu\cos\theta)}}$
問4 金属球を糸につるしバネばかりで重さをはかったところ 1.0 kgwであった。つぎに、水が入ったビーカーの中に金属球全体を浸したところ、はかりは0.80 kgwをしめした。金属球の体積はいくらか、ただし. 水の密度を1.0×10³ kg/m³とする。
- a. 2.0 cm³
- b. 8.0 cm³
- c. 20 cm³
- d. 80 cm³
- e. 200 cm³
- f. 800 cm³
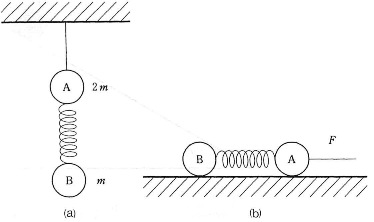
問5 質量2$m$の物体Aと質量$m$の物体Bがバネで連結されている。Aの方に糸をつけ天井からつるしたところ、バネは自然の長さから$l$ だけ伸びた(図a)。つぎにAとBをなめらかな床の上に置き、Aを$F$の力で引き加速度運動をさせた(図b)。このときのバネの伸びはいくらか、重力加速度の大きさを$g$とする。
- a. $\dfrac{mg}{F}l$
- b. $\dfrac{2mg}{F}l$
- c. $\dfrac{3mg}{F}l$
- d. $\dfrac{F}{3mg}l$
- e. $\dfrac{F}{2mg}l$
- f. $\dfrac{F}{mg}l$