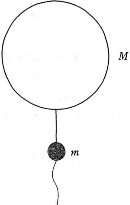
質量$M$の気球に質量$m$のおもりがつりさげられている。おもりはロープで地上に固定されている。ある時刻$t=0$にロープが切られ、気球とおもりは加速度$\alpha$で上昇を始めた。次の問6と問7に答えよ。ただし、重力加速度の大きさを$g$とする。また気球とおもりに働く空気抵抗は無視し、おもりにはたらく浮力も無視する。

• 問6 上昇を始めて$T$秒後に、質量$m$のおもりを切り離した。その後の気球の加速度はいくらになるか。
  • a. $\bigg(1+\dfrac{m}{M}\bigg)\alpha+\dfrac{m}{M}g$
  • b. $\bigg(1+\dfrac{m}{M}\bigg)\alpha-\dfrac{m}{M}g$
  • c. $\bigg(1-\dfrac{m}{M}\bigg)\alpha+\dfrac{m}{M}g$
  • d. $\bigg(1+\dfrac{m}{M}\bigg)g+\dfrac{m}{M}\alpha$
  • e. $\bigg(1+\dfrac{m}{M}\bigg)g-\dfrac{m}{M}\alpha$
  • f. $\bigg(1-\dfrac{m}{M}\bigg)g+\dfrac{m}{M}\alpha$
• 問7 おもりが切り離された後から、おもりが再び切り離されたときと同じ高さに戻るまでの時間はいくらか。
  • a. $\dfrac{\alpha}{g}T$
  • b. $2\dfrac{\alpha}{g}T$
  • c. $3\dfrac{\alpha}{g}T$
  • d. $\dfrac{g}{\alpha}T$
  • e. $2\dfrac{g}{\alpha}T$
  • f. $3\dfrac{g}{\alpha}T$