振動数$f$の音さを前に、これとわずかに異なる振動数の音さを後ろにのせた長い台車が速さ$v$で観測者に近づいてくる。観測者にはうなりが聞こえている。音速を$V$として、以下の問に答えよ。

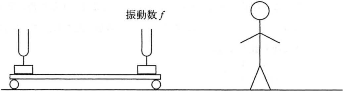
• 問13 台車の前だけが通過した後、うなりが消えた。台車の後ろに乗せた音さの振動数はいくらか。
  • a. $\dfrac{2v}{V+v}f$
  • b. $\dfrac{V-v}{V+v}f$
  • c. $\dfrac{V}{V+v}f$
  • d. $\dfrac{2v}{V-v}f$
  • e. $\dfrac{V}{V-v}f$
  • f. $\dfrac{V+v}{V-v}f$
• 問14 台車全体が通過した後に聞こえるうなりの振動数はいくらか。
  • a. $\dfrac{vV}{(V-v)^2}f$
  • b. $\dfrac{vV}{V^2-v^2}f$
  • c. $\dfrac{vV}{(V+v)^2}f$
  • d. $\dfrac{2vV}{(V-v)^2}f$
  • e. $\dfrac{2vV}{V^2-v^2}f$
  • f. $\dfrac{2vV}{(V+v)^2}f$