東邦大学物理2013年第4問
以下の問7から問9に答えよ。
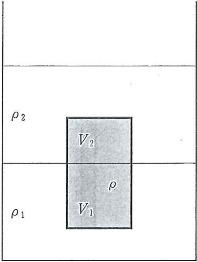
- 問7 ある大きな容器内に異なる密度$\rho_1$と$\rho_2$の2種類の液体が図のように層をなしている。この液体内に密度$\rho(\rho_1\gt \rho\gt \rho_2)$の柱状の物体を入れたところ、図のように静止した。物体の境界面に対して下の部分と上の部分の体積をそれぞれ$V_1$と$V_2$として、それらの比$V_2/V_1$はいくらか。
- (a) $\dfrac{\rho_1-\rho}{\rho_1-\rho_2}$
- (b) $\dfrac{\rho-\rho_2}{\rho_1-\rho_2}$
- (c) $\dfrac{\rho_1-\rho}{\rho-\rho_2}$
- (d) $\dfrac{\rho_1-\rho_2}{\rho-\rho_2}$
- (e) $\dfrac{\rho_1-\rho_2}{\rho_1-\rho}$
- (f) $\dfrac{\rho-\rho_2}{\rho_1-\rho}$
問8 水平に回転している大きな円板上に質量$m$の物体が置かれている。回転中心から物体までの距離は$r$である。また、物体の大きさは距離$r$に比べて十分に小さいとする。物体と円板との間の静止摩擦係数を$\mu$、重力加速度の大きさを$g$とする。
円板の回転を徐々に上げたところ、円板がある角速度$\omega$で回転しているとき物体がすべり始めた。このときの角速度はいくらか。
- (a) $\sqrt{\dfrac{\mu g}{2r}}$
- (b) $\sqrt{\dfrac{g}{2r}}$
- (c) $\sqrt{\dfrac{g}{2\mu r}}$
- (d) $\sqrt{\dfrac{\mu g}{r}}$
- (e) $\sqrt{\dfrac{g}{r}}$
- (f) $\sqrt{\dfrac{g}{\mu r}}$
- 問9 長さ$L$、質量$M$の細長い一様な板が水平でなめらかな床の上に置かれており、さらに板の端には質量$m$の車が置かれている。車が動いて板の他端に達したとき、車が床に対して移動した距離はいくらか。ただし、車の大きさは板の長さに比べて十分に小さいとする。

- (a) $\dfrac{m}{M+m}\cdot\dfrac{L}{2}$
- (b) $\dfrac{M-m}{M+m}\cdot\dfrac{L}{2}$
- (c) $\dfrac{M}{M+m}\cdot\dfrac{L}{2}$
- (d) $\dfrac{m}{M+m}\cdot L$
- (e) $\dfrac{M-m}{M+m}\cdot L$
- (f) $\dfrac{M}{M+m}\cdot L$