東邦大学物理2012年第7問

次の電磁気に関する問19から問25に答えよ。

問19 次の文章のうち正しいのを選べ。
- a. 電気力線は正の電荷から出て、負の電荷で終わる。また、電気力線は電荷のないところで突然生じたり切れたりせず、枝分かれも交差もしない。
- b. 導体に帯電体を近づけると、帯電体に近い側には帯電体と異なる符号の電荷が現れ、帯電体から速い側には帯電体と同じ符号の電荷が現れる。したがって、このとき導体内にはゼロでない電場が存在している。
- c. 電気を通さない物質を不導体といい、その物質の内部には自由電子は存在しない。したがって、不導体に帯電体を近づけても電子の移動は全く起こらず、不導体が他の電荷から電気力を受けることはない。
- d. 電位の等しい点をつないで得られる面を等電位面という。等電位面に沿って電荷を移動しても電気力は仕事をしない。したがって、電気力線は等電位面に垂直に交わっている。
- e. 導体でできた金属かごの中に入れたはく検電器に、かごの外部から帯電体を近づけても、はく検電器のはくの状態は変化しない。このように、物体を導体で囲むことによって外部の電場をさえぎることを誘電分極という。
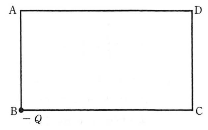
問20 図のような辺の長さの比が$1:\sqrt3$の長方形ABCDがある。頂点Bに負の電荷$-Q$ [C]を置いたとき、頂点Dにおける電場がゼロになるように順点Aと頂点Cに電荷を置いた。頂点Aに置いた電荷の大きさはいくらか。
- a. $\dfrac{3\sqrt3}{4}Q$
- b. $\dfrac{3}{4}Q$
- c. $\dfrac{\sqrt3}{4}Q$
- d. $\dfrac{3\sqrt3}{8}Q$
- e. $\dfrac{3}{8}Q$
- f. $\dfrac{\sqrt3}{8}Q$
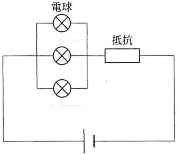
問21 電圧4.8 Vをかけたとき電力2.4 Wを消費する規格の電球がある。この電球を3個並列につないで、6.0 Vの電池で電球の規格通りに点灯したい。図のように抵抗を配置したとき抵抗値をいくらにすればよいか。値が最も近いのを選べ。
- a. 0.50 Ω
- b. 0.80 Ω
- c. 1.5 Ω
- d. 2.4 Ω
- e. 6.0 Ω
- f. 9.6 Ω
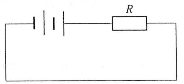
問22 内部抵抗を持つある起電力の電池1個に抵抗値$R$の低抗をつないだとき、大きさ$I_1$の電流が流れた。次に、図のようにこの電池2個を直列につなぎ、これに同じ抵抗値$R$の抵抗をつないだとき大きさ$_2$の電流が流れた。電池の内部抵抗はいくらか。
- a. $\dfrac{I_1-2I_2}{I_2-I_1}R$
- b. $\dfrac{I_2-I_1}{I_1-2I_2}R$
- c. $\dfrac{I_2-I_1}{2I_1-I_2}R$
- d. $\dfrac{I_2-2I_1}{I_2-I_1}R$
- e. $\dfrac{2(I_2-I_1)}{2I_1-I_2}R$
- f. $\dfrac{2I_1-I_2}{2(I_2-I_1)}R$
問23 初速度を0として、電圧$V$で加速された電子が一様な磁束密度$B$の磁場に、磁場に垂直に入射した。電子の質量を$m$、電荷の大きさを$e$として、電子が描く円軌道の半径はいくらか。
- a. $\dfrac{1}{2B}\sqrt{\dfrac{mV}{2e}}$
- b. $\dfrac{1}{2B}\sqrt{\dfrac{mV}{e}}$
- c. $\dfrac{1}{B}\sqrt{\dfrac{mV}{2e}}$
- d. $\dfrac{1}{B}\sqrt{\dfrac{mV}{e}}$
- e. $\dfrac{1}{B}\sqrt{\dfrac{2mV}{e}}$
- f. $\dfrac{2}{B}\sqrt{\dfrac{mV}{e}}$
問24 図のような一様な磁場の領域を導線でできている長方形回路ABCDが右向きに通り過ぎようとしている。磁場は紙面表から裏に向かっている。下記の文のうちで正しいのをすべて選べ。
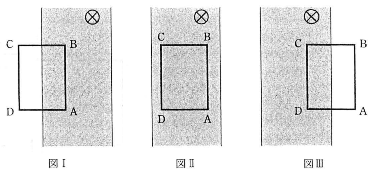
- a. 図$\text{I}$のときに生じている誘導電流の向きは反時計回り(ABCDAの順)である。
- b. 図$\text{I}$のときに生じている誘導電流の向きは時計回り(ADCBAの順)である。
- c. 図$\text{I}\hspace{-.1em}\text{I}$のときに生じている誘導電流の向きは反時計回り(ABCDAの順)である。
- d. 図$\text{I}\hspace{-.1em}\text{I}$のときに生じている誘導電流の向きは時計回り(ADCBAの順)である。
- e. 図$\text{I}\hspace{-.1em}\text{I}\hspace{-.1em}\text{I}$のときに生じている誘導電流の向きは反時計回り(ABCDAの順)である。
- f. 図$\text{I}\hspace{-.1em}\text{I}\hspace{-.1em}\text{I}$のときに生じている誘導電流の向きは時計回り(ADCBAの順)である。
問25 ある変圧器は実効値3.0×10³ Vの1次側交流電圧を実効値1.0×10² Vの2次側交流電圧に変えている。2次側に抵抗値20Ωの抵抗をつないで電流を流したとき、1次側に流れる電流はいくらか。値が最も近いのを選べ。ただし、電力の損失はないものとする。
- a. 6.7×10^－3 A
- b. 0.17 A
- c. 5.0 A
- d. 6.0 A
- e. 30 A
- f. 1.5×10² A