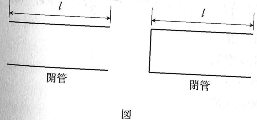
空気中に置かれた図のような長さ$l$[m]の開管と閉管がある。これらの管内の気柱を伝わる音波がつくる定常波について以下の各問いに答えなさい。答えは各問いの解答群の中から最も適切なものを一つ選び、解答欄の記号にマークしなさい。ただし、開口端と定常波の腹の位置とは一致するものとし、必要があれば温度$t$[℃]のときの空気中の音速$v$[m/s]を求める式、$v=331.5+0.6t$を用いなさい。
| 気体 | 音速[m/s] |
| 空気 | 331.5 |
| 二酸化炭素 | 258 |
| ヘリウム | 970 |
はじめに2つの管を温度$0$℃の空気中においた。
- (1) 開管と閉管にできる定常波の基本振動数が$\Delta f$[Hz]であった。開管および閉管の長さ$l$[m]を求めなさい。
- (2) 開管にできる定常波の2倍振動と閉管にできる3倍振動の場合の波長の差は何mか。
- (3) 開管を$0$℃の空気中においた場合、$0$℃の二酸化炭素中においた場合、$0$℃のヘリウム中においた場合で、基本振動数の定常波ができるとき、振動数の大きさの順序はどのようになるか。ただし、$0$℃のときの各気体の音速は表の通りである。
次に、空気中に置かれた開管と気柱の温度を$t_1$[℃]に上昇させた。
- (4) 温度が$t_1$[℃]の場合と$0$℃の場合の開管にできる定常波の基本振動数の差は何Hzか。ただし、ここでは管の熱膨張は考えないものとする。
- (5) 温度上昇に伴う開管の熱膨張を考慮してみよう。温度上昇によっても定常波の基本振動数が$0$℃の場合と変わらないようにするには、管の線膨張率$\alpha$[1/K]はどのくらいの値が必要か。最も近いものを求めなさい。
〔解答群〕
- (1)
- (ア) $0$
- (イ) $\dfrac{331.5}{4\Delta f}$
- (ウ) $\dfrac{331.5}{2\Delta f}$
- (エ) $\dfrac{331.5}{\Delta f}$
- (オ) $\dfrac{663}{\Delta f}$
- (2)
- (ア) $0$
- (イ) $\dfrac{1}{4}l$
- (ウ) $\dfrac{1}{3}l$
- (エ) $l$
- (オ) $2l$
- (3)
- (ア) へリウム$\gt$二酸化炭素$\gt$空気
- (イ) 二酸化炭素$\gt$空気$\gt$へリウム
- (ウ) へリウム$\gt$空気$\gt$二酸化炭素
- (エ) 空気$\gt$二酸化炭素$\gt$へリウム
- (オ) 気体の種類によって変わらない
- (4)
- (ア) $\dfrac{331.5t_1}{l}$
- (イ) $\dfrac{0.6t_1}{4l}$
- (ウ) $\dfrac{0.6t_1}{2l}$
- (エ) $\dfrac{331.5t_1}{2l}$
- (オ) $\dfrac{331.5t_1}{4l}$
- (5)
- (ア) $0.05$
- (イ) $0.02$
- (ウ) $0.005$
- (エ) $0.002$
- (オ) $0.0005$