東海大学物理2012年第3問
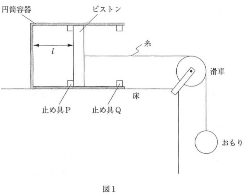
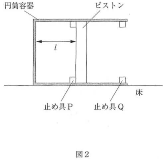
大気中で、床に固定された円筒容器に、なめらかに動く軽いピストンで$n$[mol]の単原子分子の理想気体を封じた。このときの気体の圧力は大気圧$p_0$[Pa]に等しかった。次に、軽い糸をピストンに取り付け、糸の一方の端を滑らかに回る滑車に通し、糸が床に平行となるように保った状態で質量$m$[kg]のおもりをぶら下げた。その結果図1のように、ピストンは円筒容器の底から$l$[m]の位置で静止した。その後、小さな体積の無視できる止め具Pをピストンに接する位置で円筒容器内部に固定し、糸を切り離したところ、図2のように、ピストンは止め具Pに接して静止していた。このときの気体の状態をAとし、気体の温度を$T_A$[K]とする。
次に、円筒容器に封じた気体をゆっくりと加熱し始めたところ、気体の温度が$T_B$[K]のときにピストンが右に動き始めた。この動き始めたときの気体の状態をBとする。
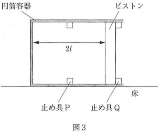
さらに気体をゆっくりと加熱し続けたところ、図3に示すようにピストンが円筒容器内部に固定された止め具Qに接触して停止した。接触したときの気体の状態をCとする。状態Cのとき、ピストンは円筒容器の底から$2l$[m]の位置にあり、気体の温度は$T_C$[K]であった。
ピストンが止め具Qに接した状態で、再び同じおもりをピストンに糸でつなぎ、気体をゆっくりと冷却した。しばらくすると気体の温度が$T_D$[K]となり、ピストンが左へ動き始めた。動き始めたときの気体の状態をDとする。
さらに気体をゆっくりと冷却したところ、気体の状態はAに戻った。
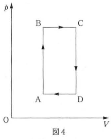
図4は、気体が上記の循環過程A→B→C→D→Aをたどる間の気体の圧力$p$[Pa]と体積$V$[m3]の関係を示している。円筒容器の内部の断面積を$S$[m2]、気体定数を$R$[J/(mol・K)]、重力加速度の大きさを$g$[m/s2]とし、以下の各問いに答えなさい。答えは各問いの解答群の中から最も適切なものを一つ選び、解答欄の記号にマークしなさい。
- (1) 温度$T_A$を求めなさい。
- (2) 温度$T_B$を求めなさい。
- (3) 温度$T_C$を求めなさい。
- (4) 温度$T_D$を求めなさい。
- (5) 気体の状態がBからCに移る過程において円筒容器内の気体がした仕事を求めなさい。
- (6) 気体の状態がDからAに移る過程において円筒容器内の気体がした仕事を求めなさい。
- (7) 循環過程A→B→C→D→Aの熱効率を求めなさい。
- (1)
- ア.$p_0\dfrac{Sl}{nR}$
- イ.$\dfrac{mgl}{nR}$
- ウ.$\left(p_0-\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- エ.$\left(p_0+\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- オ.$2p_0\dfrac{Sl}{nR}$
- (2)
- ア.$p_0\dfrac{Sl}{nR}$
- イ.$\dfrac{mgl}{nR}$
- ウ.$\left(p_0-\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- エ.$\left(p_0+\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- オ.$2p_0\dfrac{Sl}{nR}$
- (3)
- ア.$p_0\dfrac{Sl}{nR}$
- イ.$\dfrac{2mgl}{nR}$
- ウ.$2\left(p_0-\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- エ.$2\left(p_0+\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- オ.$2p_0\dfrac{Sl}{nR}$
- (4)
- ア.$p_0\dfrac{Sl}{nR}$
- イ.$\dfrac{2mgl}{nR}$
- ウ.$2\left(p_0-\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- エ.$2\left(p_0+\dfrac{mg}{S}\right)\dfrac{Sl}{nR}$
- オ.$2p_0\dfrac{Sl}{nR}$
- (5)
- ア.$p_0Sl$
- イ.$mgl$
- ウ.$\left(p_0-\dfrac{mg}{S}\right)Sl$
- エ.$\left(p_0+\dfrac{mg}{S}\right)Sl$
- オ.$2p_0Sl$
- (6)
- ア.$-p_0Sl$
- イ.$-mgl$
- ウ.$-\left(p_0-\dfrac{mg}{S}\right)Sl$
- エ.$-\left(p_0+\dfrac{mg}{S}\right)Sl$
- オ.$-2p_0Sl$
- (7)
- ア.$\dfrac{2mg}{3mg+5p_0S}$
- イ.$\dfrac{2(mg+p_0S)}{3mg+5p_0S}$
- ウ.$\dfrac{2mg}{3mg+3p_0S}$
- エ.$\dfrac{2mg+4p_0S}{3mg+5p_0S}$
- $\dfrac{4p_0S}{3mg+5p_0S}$