一般に、純粋な金属の電気抵抗は、金属内を電場の逆向きに流れる電荷$-e$の自由電子が熱運動 する金属イオンに散乱されることにより生じる。以下の問いに答えよ。

• (I) 金属イオンの熱運動を単振動するばね振り子として考えよう。
  • 問1. ばね定数$K$のばねにつけた質量$m$の物体が$x$方向に運動するとき、釣り合いの位置からの変位が$x$のときの物体の速度を$v_x$として、力学的エネルギー$E_x$を書きなさい。
  • 問2. 振り子の運動エネルギーと位置エネルギーの時間平均は等しくなる。この事実を用いて、変位の二乗の時間平均$\lt{x^2}\gt$を力学的エネルギー$E_x$を用いて表しなさい。
  • 問3. 導体内の金属イオンは$x$方向だけでなく$y$、$z$方向にも運動をしているから、金属イオンの平衡位置からの変位ベクトルを$(x,~y,~z)$、変位半径を$r\left(=\sqrt{x^2+y^2+z^2}\right)$とする。また、金属イオンの熱運動は$x$、$y$、$z$の各方向に同等(等方的)であるとして、変位半径の二乗の時間平均$\lt{r^2}\gt$を$x$方向の力学的エネルギー$E_x$を用いて表しなさい。
  • 問4. 金属イオンの運動は気体分子の運動と同じように熱エネルギーによるもので、金属イオンの平均運動エネルギーは単原子気体分子の平均運動エネルギーに等しい。このことから、導体が絶対温度$T$にあるとき、金属イオンの平均の力学的エネルギーを求めなさい。ただし、ボルツマン定数を$k_B$とする。
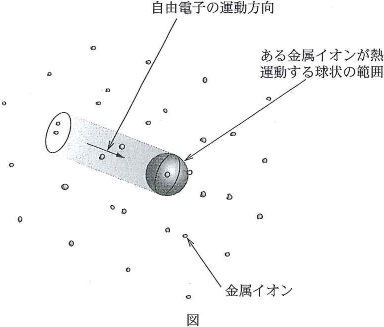
  • 問5. 問題を簡単にするために、図のように、1つの金属イオンは熱運動している球状の範囲を通る電子を散乱すると考える。すなわち、電場の影響で一方向に一様に流れる自由電子は、1つの熱運動する金属イオンにより、そのイオンの二乗平均変位半径、$\sqrt{\lt{r^2}\gt}$を半径とする球状の範囲を自由電子の運動方向から見た円形の範囲で散乱されると考える。この円形の範囲の面積$A$を絶対温度$T$を用いて表しなさい。
• (II) 断面積$S$、長さ$L$の(I)で考えた導体の両端に電圧$V$を加えたとき、散乱されながら運動する電子を考える。
  • 問1. この導体中の電場は一様であるとして、電場の大きさを求めなさい。
  • 問2. 電荷$-e$の自由電子は一様な電場の中を金属イオンに散乱されながら運動する。金属イオンによる散乱は、平均として電子の電場方向の速さ$v$に比例し、運動方向に逆向きの抵抗力を電子におよぼす。抵抗力は(I)問5で求めた面積$A$に比例すると考えられ、$k$を比例定数としてその大きさは$kAv$と与えられる。電流が定常的に流れている場合、自由電子は平均として一定の速度で運動するようになっていると考えられる。その速度を温度の関数として求めなさい。
  • 問3. 導体中の電子数密度を$n$とするとき、この導体を流れる定常電流を求めなさい。
  • 問4. この導体の抵抗$R$を絶対温度$T$を用いて表しなさい。
• (III) (II)で考えた導体に電流を流したときに発生するジュール熱と導体の温度との関係について考える。この導体は単位時間あたりに$Q$[J/s]の割合で熱を周囲に放射する。絶対温度$T$のとき、$Q$は以下のように与えられる。 \[Q=aT^4\] ただし、$a$は定数である。ジュール熱と熱放射以外にこの導体からの熱の発生、損失はないものとして以下の問いに答えなさい。
  • 問1. 両端に電圧$V$を加え、この導体の絶対温度が$T$に保たれているとき、単位時間あたりに発生するジュール熱を求めなさい。
  • 問2. この導体の温度が一定になった状態では、絶対温度$T$、電流$I$は電圧$V$に対し、 \[T=bV^p、I=cV^q\] のように変化する。定数$p$、$q$を求めなさい。ただし、$b$、$c$は導体によって決まる定数である。