東京慈恵会医科大学物理2013年第1問
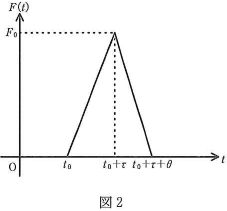
- (I) 図1のように質量$m$、半径$a$の球形のゴムボールを高さ$h$のところから水平な床に初速$0$で落下させたときの運動を考える。床がボールから受けた力は時刻$t$に対して図2のように直線的に変化した。ただし、ボールが落下し始めた時を時刻$0$としており、$\theta\lt\tau$である。重力加速度の大きさを$g$とし、空気の抵抗、ボールの回転はないものとして次の問いに答えよ。
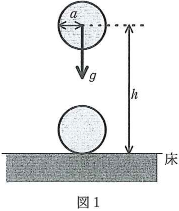
- 問1. ボールが落下し、初めて床に接触するときの速さを求めなさい。
- 問2. 図2の$t_0$を求めなさい。
- 問3. 図2の$t=t_0+\tau$のとき、ボールは一旦静止する。このことから$F_0$を$g$、$h$などを用いて表しなさい。
- 問4. ボールが床から離れる瞬間の速さを$g$、$h$などを用いて表しなさい。
- 問5. この衝突での反発係数を求めなさい。
- 問6. 衝突の前後での力学的エネルギーの変化を求めなさい。
- (II) 図3のように、動摩擦係数$\mu’$の水平な床に、質量$m$のボールが入射角$\theta(0^\circ\lt\theta\lt 90^\circ)$、速さ$v$で衝突し、反射角$\theta’(0^\circ\lt\theta’\lt 90^\circ)$、速さ$v’$ではねかえる運動を考える。ボールが床に接触している時間$\Delta t$の間にボールは床から一定の大きさ$R$の垂直抗力を受けるとして、以下の問いに答えなさい。ただし、空気による抵抗、重力は無視できるものとし、床とボールの反発係数を$e$とせよ。
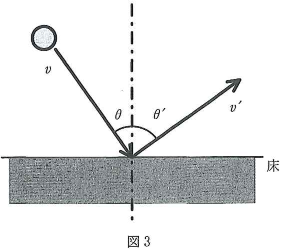
- 問1. 床に平行な方向と垂直な方向それぞれについて、ボールの運動量の変化についての方程式を書きなさい。ただし、向きは平行成分、垂直成分ともに衝突後の向きを正とする。
- 問2. $\tan\theta’$を$\tan\theta$、$\mu’$、$\theta$を用いて表しなさい。