• 問 1. 雨粒の速度が鉛直方向に$v_\perp$ [m/s]、水平方向に$v_\|$ [m/s]であるとき、雨粒の鉛直方向の加速度を$a_\perp$ [m/s²]、水平方向の加速度を$a_\|$ [m/s²]として、鉛直方向、水平方向それぞれの運動方程式を書け。ただし、鉛直方向については重力の向きを負の向きとする。
• 問 2. 雨粒が十分に高い所から落下する場合、地表近くでは等速運動すると考えられる。そのときの速度(終端速度)の鉛直成分および水平成分を求めよ。
• 問 3. 時間雨量*が$l$ [mm]である雨が継続的かついたるところ一様に降るとする。雨の質量密度を$\rho$ [kg/m³]とするとき、平均として1秒あたり、1m²あたりに降る雨粒の数を求めよ。

  *時間雨量とは1時間あたりに降った雨が溜まった深さをmm単位で表記したものである。

• 問 4. 前問の状況の雨が水平な屋根に一様に降るとき、雨粒は屋根に落ちた瞬間付着し、跳ねることはないとする。このとき、雨粒は終端速度に達しているとし、その大きさを$v_\infty$として、雨粒が屋根に及ぼす平均の圧力を求めよ。ただし、屋根に水が溜まることはないものとする。

半径$r$ [m]の半球形の屋根が高さ$r$の円柱部分の上に乗っている。屋根は超撥水性素材でできており、雨粒は球状になって表面を滑る。屋根の最高点$\text{P}$のごく近くに落ちた雨粒が滑り落ちることを考える。以下の問題では、雨粒の初期位置は最高点$\text{P}$、初速度の大きさは0、質量$m$ [kg]として答えよ。ただし、雨粒と屋根との間の摩擦力. 空気による抵抗力は無視できるものとし、重力加速度の大きさを$g$ [m/s²]とする。

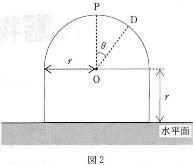
• 問 1. 雨粒が屋根から離れずに運動し、屋根上の点$\text{D}$を通るとき、屋根から受ける力の大きさを$m$、$g$、$\theta$で表せ、ただし、$\angle\text{POD}=\theta$ [rad]とする。
• 問 2. 雨粒が屋根から離れる点を点$\text{D}$とすると、$\tan\theta$はいくらか。
• 問 3. 雨粒が水平面に落下する点と点$\text{P}$との水平距離を求めよ。