次の電流と磁場(磁界)に関する問いに答えよ。ただし、全ての系は真空中にあり、真空の透磁率は$\pi$を円周率として、$\mu_0=4\pi\times10^{-7}$ [H/m$=$N/A²]で与えられる。

• (Ⅰ) 図1のように、$xyz$座標の$x$軸に沿って正の向きに電流$I_1$ [A]、$y$軸に沿って正の向きに電流$I_2$ [A]が流れている. これらの電流によって周囲に作られる磁場を考える。
  
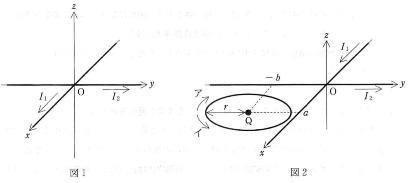
  • 問 1. $z$軸上の点$\text{P}(0,~0,~z)$ ($z$の単位はメートル)における磁場を3次元ベクトルで表せ。
  • 問 2. 磁場の強さが0となる点の集合が作る図形の方程式を求めよ. ただし、$x$、$y$軸上は考慮しないものとする。
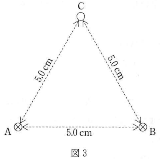
  • 問 3. 図2のように、点$\text{Q}(a,-b,~0)(a,b\gt0)$を中心とする半径$r (r\lt a,~r\lt b)$の1巻きコイルが$xy$平面上に置かれている、点$\text{Q}$の磁場の強さを0にするために、コイルに流すべき電流の大きさと向きを求めよ、ただし. 電流の向きは図2のアかイで答えよ。
• (Ⅱ) 図3のように、1辺の長さ5.0 cmの正三角形の各頂点に、3本の導線A、B、Cが互いに平行に張られ、A、Bにいずれも紙面に垂直に表から裏へ向かう向きに、2.0 A(アンペア)の電流が流れている。
  
  • 問 1. 導線Cの位置の磁場の強さと向きを求めよ。
  • 問 2. 導線Cにも同じ向きに2.0 Aの電流を流すと、導線Cに働く力の1.0 mあたりの大きさと向きを求めよ。